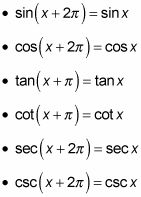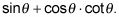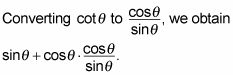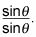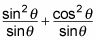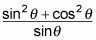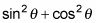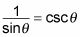¿Cómo simplificar una expresión utilizando identidades periodicidad
Identidades Periodicidad ilustrar cómo trasladar la gráfica de una función trigonométrica por un período a los resultados de izquierda o derecha en la misma función. Las funciones de seno, coseno, secante, cosecante y repetir cada 2 (pi) tangente unidades- y cotangente, por el contrario, se repiten cada unidades pi.
Las siguientes identidades muestran cómo las diferentes funciones trigonométricas repiten:
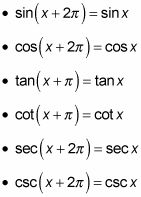
Puede utilizar identidades periodicidad para simplificar expresiones. Identidades similares a la co-función, se utilizan las identidades periodicidad cuando vea
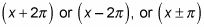
dentro de una función trigonométrica. Debido a la adición (o restar) 2 (pi) radianes de un ángulo le da una nueva perspectiva en la misma posición, puede utilizar esa idea de formar una identidad. Por la tangente y sólo cotangente, sumar o restar pi radianes del ángulo que da el mismo resultado, ya que el período de las funciones tangente y cotangente es pi.
Por ejemplo, para simplificar
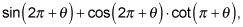
sigue estos pasos:
Vuelva a colocar todas las funciones trigonométricas con 2 (pi) - o pi en el caso de la cotangente - dentro de los paréntesis con la identidad periodicidad adecuada.
Para este ejemplo,
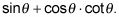
Simplifique la nueva expresión.
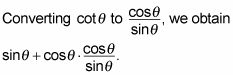
Para encontrar un denominador común para agregar las fracciones, multiplique el primer término por
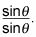
Aquí está la nueva fracción:
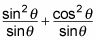
Añadir a una para conseguir esto:
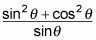
Usted puede ver una identidad de Pitágoras en el numerador, por lo reemplace
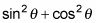
con 1. Por lo tanto, la fracción se convierte
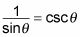
Sobre el autor
 ¿Cómo simplificar una expresión utilizando par / impar identidades
¿Cómo simplificar una expresión utilizando par / impar identidades Debido seno, coseno, y la tangente son funciones (funciones trigonométricas), que pueden definirse como pares o impares funciones. Sine y la tangente son funciones impares, y el coseno es una función par. En otras palabras,pecado(-X) = -sen Xcos…
 ¿Cómo simplificar una expresión utilizando identidades de función co-
¿Cómo simplificar una expresión utilizando identidades de función co- Si usted toma la gráfica de y = Sen X y desplazar hacia la izquierda por pi / 2 unidades, se ve exactamente como la gráfica de y = Cos X. Lo mismo es cierto para la tangente y cotangente, así como secante y cosecante. Esa es la premisa básica de…
 ¿Cómo simplificar una expresión utilizando identidades recíprocas
¿Cómo simplificar una expresión utilizando identidades recíprocas Cuando se le pregunta para simplificar una expresión que implica cosecante, secante o cotangente, cambia la expresión de funciones que implican seno, coseno, tangente o, respectivamente. Al cambiar las funciones de esta manera, usted está…
 Cómo utilizar identidades para integrar las funciones trigonométricas
Cómo utilizar identidades para integrar las funciones trigonométricas Usted se sorprenderá de lo mucho que avanzar a menudo se puede hacer cuando se integra una función de trigonometría desconocida por primera ajustar usando las identidades Básica Cinco trig:El poder invisible de estas identidades se encuentra en…
 Cotangente y cosecante identidades en un círculo unitario
Cotangente y cosecante identidades en un círculo unitario A partir de la identidad de Pitágoras, el pecado2theta- + cos2theta- = 1, puede derivar cotangente y cosecante identidades pitagóricas. Todo lo que hacemos es tirar un poco de álgebra y aplicar las identidades recíprocas y de relación y -…
 Tratar con identidades medio-ángulo que involucran radicales
Tratar con identidades medio-ángulo que involucran radicales Mediante la adición, sustracción, o duplicando medidas de los ángulos, se puede encontrar gran cantidad de valores exactos de las funciones trigonométricas. Por ejemplo, puede utilizar la identidad de medio ángulo cuando el valor exacto de la…
 Gama de funciones trigonométricas tangente y cotangente Dominio y
Gama de funciones trigonométricas tangente y cotangente Dominio y La tangente y cotangente están relacionadas no sólo por el hecho de que son recíprocos, sino también por el comportamiento de sus rangos. En referencia al plano de coordenadas, tangente es y/X, y cotangente es X/y. Los dominios de ambas…
 Sine Express en términos de secante o cosecante
Sine Express en términos de secante o cosecante A pesar de que cada función trigonométrica es perfectamente maravilloso, poder expresar cada función trig en términos de una de las otras cinco funciones trigonométricas es con frecuencia a su ventaja. Por ejemplo, usted puede tener algunos…
 Sine Express en términos de cotangente
Sine Express en términos de cotangente A pesar de que cada función de la trigonometría es perfectamente maravilloso, poder expresar cada función trig en términos de una de las otras cinco funciones trigonométricas es con frecuencia a su ventaja. Por ejemplo, usted puede tener…
 Encuentra identidades trigonométricas opuesto ángulo
Encuentra identidades trigonométricas opuesto ángulo los identidades de ángulo opuesto cambiar las funciones trigonométricas de ángulos negativos a las funciones de ángulos positivos. Ángulos negativos son grandes para describir una situación, pero no son realmente útil cuando se trata de pegar…
 Encuentra identidades relación trigonometría
Encuentra identidades relación trigonometría Trig tiene dos identidades llamados identidades de relación. Esta etiqueta puede ser confuso, ya que todas las funciones trigonométricas se definen por relaciones. En algún momento, sin embargo, los matemáticos pensaron que esta descripción era…
 ¿Cómo encontrar identidades medio-ángulo para tangente
¿Cómo encontrar identidades medio-ángulo para tangente La media de ángulo trig identidad para tangente tiene dos versiones. En lugar de que esto sea una molestia, que tiene más de una opción es realmente bastante agradable, porque se puede elegir la versión que mejor se adapte a su situación. Las…