Tratar con identidades medio-ángulo que involucran radicales
Mediante la adición, sustracción, o duplicando medidas de los ángulos, se puede encontrar gran cantidad de valores exactos de las funciones trigonométricas. Por ejemplo, puede utilizar la identidad de medio ángulo cuando el valor exacto de la función trigonométrica implica radicales.
Este ejemplo utiliza bronceado PI / 8:
Determine qué ángulo es el doble del ángulo que se está trabajando.
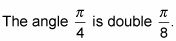
Sustituir la medida del ángulo en una de las identidades tangentes-media angulares.
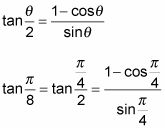
Rellene los valores de la función y simplificar la respuesta.
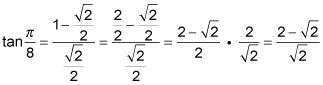
Para obtener el cabo radical del denominador, racionalizarlo multiplicando ambas partes de la fracción por el radical.
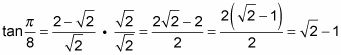
La otra identidad para la tangente de un ángulo medio le da exactamente la misma respuesta. Esa forma no es nada fácil, sin embargo, debido a que tanto el seno y el coseno de ese ángulo tienen un radical en ellos. Si el problema involucrado un ángulo de 60 grados, sin embargo, la historia sería diferente. El seno de 60 grados es
y el coseno es 1/2, que prácticamente le ruega que utilice el formulario con el coseno en el denominador por lo que no tiene que meterse con un radical en el denominador. Ambas identidades funcionan - la que utiliza es sólo una cuestión de preferencia personal.
-
Más allá de lo básico con identidades trigonométricas -
Cómo calcular los valores para las seis funciones trigonométricas -
¿Cómo encontrar la tangente de la suma o diferencia de ángulos -
¿Cómo encontrar funciones trigonométricas de un ángulo utilizando identidades pitagóricas -
¿Cómo simplificar una expresión utilizando identidades periodicidad -
Cómo utilizar identidades medio ángulo para evaluar una función trigonométrica
Gama de funciones seno y coseno de dominio y Las funciones seno y coseno son únicos en el mundo de las funciones trigonométricas, porque sus relaciones siempre tienen un valor. No importa desde qué ángulo lo de entrada, se obtiene una salida resultante. El valor que se obtiene puede ser 0,…
Encuentra identidades trigonométricas opuesto ángulo los identidades de ángulo opuesto cambiar las funciones trigonométricas de ángulos negativos a las funciones de ángulos positivos. Ángulos negativos son grandes para describir una situación, pero no son realmente útil cuando se trata de pegar…
¿Cómo encontrar identidades medio-ángulo para tangente La media de ángulo trig identidad para tangente tiene dos versiones. En lugar de que esto sea una molestia, que tiene más de una opción es realmente bastante agradable, porque se puede elegir la versión que mejor se adapte a su situación. Las…
Cómo eliminar un tercer ángulo para resolver una identidad trigonometría Identidades de suma y diferencia por lo general implican dos ángulos diferentes y luego un tercer ángulo combinado. Al probar estas identidades trigonométricas, a menudo es necesario deshacerse de ese tercer ángulo. El siguiente ejemplo trata de…
¿Cómo resolver una ecuación trigonométrica que tiene múltiples funciones trigonométricas Algunas ecuaciones de trigonometría contienen más de una función trigonométrica. Otros tienen mezclas de múltiples ángulos y ángulos individuales con la misma variable. Algunos ejemplos de tales ecuaciones incluyen 3cos2 X = Sen2 X, 2 seg X =…
¿Cómo resolver funciones trigonométricas inversas con ángulos poco comunes Cuando se trabaja con funciones trigonométricas inversas, siempre es más conveniente cuando los números que está trabajando son los resultados de la aplicación de una de las funciones trigonométricas a una medida de ángulo común. Cuando el…
Cómo utilizar identidades medio ángulo para encontrar el seno de un ángulo Mediante la adición, sustracción, o duplicando medidas de los ángulos, se puede encontrar gran cantidad de valores exactos de las funciones trigonométricas utilizando las funciones de ángulos que ya conoce. Por ejemplo, a pesar de que se puede…
Cómo utilizar la identidad de ángulo suma, cuando usted no sabe el ángulo En algunos problemas de trigonometría, usted no puede saber lo que la medida de un ángulo es, pero usted sabe algo acerca de valores de la función del ángulo. Por ejemplo, suponga que tiene dos ángulos, alfa en el segundo cuadrante de un…
Cómo utilizar la identidad de doble ángulo para el seno La fórmula de doble ángulo para el seno proviene del uso de la identidad trigonométrica para el seno de una suma, el pecado (alfa + beta-) = sinalpha-cosbeta- +-cosalpha sinbeta-. Si alfa = beta-, entonces se puede sustituir beta- con alfa en la…
Cómo utilizar las identidades de resta en un problema trig Usted puede encontrar valores de la función de los ángulos utilizando identidades ángulo de adición. Y usted tiene más posibilidades de encontrar los valores de la función de los ángulos cuando se utiliza la resta en un problema de…
¿Cómo trabajar con funciones trigonométricas inversas La forma más fácil de trabajar con funciones trigonométricas inversas es tener una práctica tabla con los valores exactos de las funciones. Cuando ángulos distintos de los más comunes o populares están involucrados, puede utilizar una tabla o…
Identificar ángulos coterminales Dos ángulos son coterminal si tienen el mismo lado terminal. Usted tiene un número infinito de formas de dar una medida de ángulo de un rayo terminal en particular. A veces, el uso de un ángulo negativo en lugar de un ángulo positivo es más…