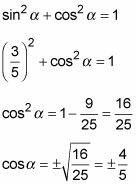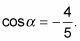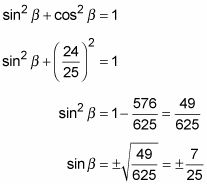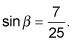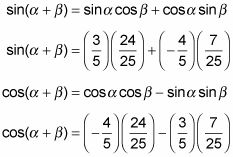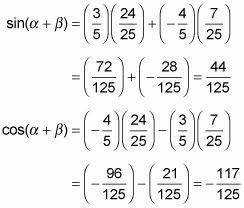Cómo utilizar la identidad de ángulo suma, cuando usted no sabe el ángulo
En algunos problemas de trigonometría, usted no puede saber lo que la medida de un ángulo es, pero usted sabe algo acerca de valores de la función del ángulo. Por ejemplo, suponga que tiene dos ángulos, alfa en el segundo cuadrante de un círculo unitario, y beta- en el primer cuadrante.
Encuentra todos los valores de la función necesaria para las sumas.
Tanto las identidades ángulo de suma de seno y coseno utilizar tanto el seno y el coseno de cada ángulo en cuestión. Usted ya sabe el seno de un ángulo y el coseno del otro ángulo, así que hay que determinar el coseno y seno desconocido - puede hacerlo mediante el uso de la identidad de Pitágoras:
En primer lugar, utilizar el valor para sinalpha- para resolver cosbeta-:
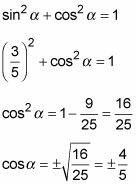
Se termina con dos resultados. Debido a que el lado terminal del ángulo alfa está en el segundo cuadrante, el coseno de alfa-, en este caso, es negativo:
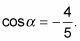
Ahora usa el valor para cosbeta- para resolver sinbeta-:
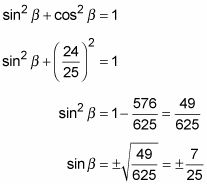
El lado del terminal de ángulo beta- es en el primer cuadrante, donde el seno es positivo:
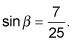
Introducir los valores de la función en las identidades para el seno y el coseno de la suma de los ángulos.
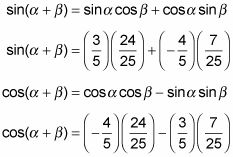
Simplifique las identidades y resolver por las respuestas.
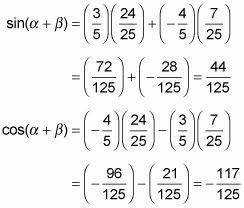
Al observar las medidas de los ángulos, se puede predecir si el valor de la función será positivo o negativo. En el ejemplo anterior, los ángulos más pequeños, cuando se añaden juntos, crean un ángulo con su lado terminal en el segundo cuadrante. El seno de un ángulo en el segundo cuadrante es positivo. Así que no es ninguna sorpresa que el seno viene a ser un valor positivo y, asimismo, que el coseno es un valor negativo (porque coseno es negativo en el segundo cuadrante).
-
La aplicación de las fórmulas de suma y diferencia de los cosenos para encontrar el coseno de la suma o diferencia de dos ángulos -
Cómo calcular los valores para las seis funciones trigonométricas -
¿Cómo encontrar funciones trigonométricas de un ángulo utilizando identidades pitagóricas -
Cómo graficar una función tangente -
Cómo utilizar identidades medio ángulo para evaluar una función trigonométrica -
Asignar valores de la función trigonométrica negativos y positivos por cuadrante
Asignar funciones trigonométricas negativos y positivos por cuadrante Los valores de seno para 30, 150, 210 y 330 grados son 1/2, 1/2, -1/2 y -1/2, respectivamente. Todos estos múltiplos de 30 grados tienen un pecado cuyo valor absoluto del medio. La siguiente regla y figura ayudarle a determinar si un valor…
Tratar con identidades medio-ángulo que involucran radicales Mediante la adición, sustracción, o duplicando medidas de los ángulos, se puede encontrar gran cantidad de valores exactos de las funciones trigonométricas. Por ejemplo, puede utilizar la identidad de medio ángulo cuando el valor exacto de la…
Gama de funciones seno y coseno de dominio y Las funciones seno y coseno son únicos en el mundo de las funciones trigonométricas, porque sus relaciones siempre tienen un valor. No importa desde qué ángulo lo de entrada, se obtiene una salida resultante. El valor que se obtiene puede ser 0,…
Encuentra identidades trigonométricas opuesto ángulo los identidades de ángulo opuesto cambiar las funciones trigonométricas de ángulos negativos a las funciones de ángulos positivos. Ángulos negativos son grandes para describir una situación, pero no son realmente útil cuando se trata de pegar…
Cómo calcular los ángulos de referencia en grados Despejando el ángulo de referencia en grados es mucho más fácil que tratar de determinar una función trigonométrica del ángulo original. Para calcular la medida (en grados) del ángulo de referencia para cualquier ángulo theta dado, utilizar…
¿Cómo encontrar identidades medio-ángulo para tangente La media de ángulo trig identidad para tangente tiene dos versiones. En lugar de que esto sea una molestia, que tiene más de una opción es realmente bastante agradable, porque se puede elegir la versión que mejor se adapte a su situación. Las…
Encontrar la función de la trigonometría de un ángulo en un círculo unitario Puede determinar las funciones trigonométricas de cualquier ángulo que se encuentran en el círculo unitario - cualquiera que se grafican en posición estándar (es decir, el vértice del ángulo está en el origen, y el lado inicial se encuentra…
Cómo localizar ángulos de referencia Cada uno de los ángulos en un círculo unidad tiene un ángulo de referencia, que es siempre un ángulo agudo positivo (excepto los ángulos que ya son positivas y aguda). Al identificar el ángulo de referencia, se puede determinar los valores de…
¿Cómo resolver funciones trigonométricas inversas con ángulos poco comunes Cuando se trabaja con funciones trigonométricas inversas, siempre es más conveniente cuando los números que está trabajando son los resultados de la aplicación de una de las funciones trigonométricas a una medida de ángulo común. Cuando el…
Cómo utilizar identidades medio ángulo para encontrar el seno de un ángulo Mediante la adición, sustracción, o duplicando medidas de los ángulos, se puede encontrar gran cantidad de valores exactos de las funciones trigonométricas utilizando las funciones de ángulos que ya conoce. Por ejemplo, a pesar de que se puede…
Cómo utilizar la identidad de doble ángulo para el seno La fórmula de doble ángulo para el seno proviene del uso de la identidad trigonométrica para el seno de una suma, el pecado (alfa + beta-) = sinalpha-cosbeta- +-cosalpha sinbeta-. Si alfa = beta-, entonces se puede sustituir beta- con alfa en la…
¿Cómo trabajar con funciones trigonométricas inversas La forma más fácil de trabajar con funciones trigonométricas inversas es tener una práctica tabla con los valores exactos de las funciones. Cuando ángulos distintos de los más comunes o populares están involucrados, puede utilizar una tabla o…