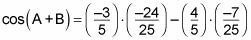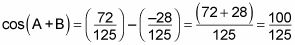La aplicación de las fórmulas de suma y diferencia de los cosenos para encontrar el coseno de la suma o diferencia de dos ángulos
Puede utilizar las fórmulas de suma y diferencia de coseno para calcular el coseno de las sumas y diferencias de ángulos de manera similar a la forma en que puede utilizar las fórmulas de suma y diferencia de seno, porque las fórmulas son muy similares entre sí. Cuando se trabaja con senos y cosenos de sumas y diferencias de ángulos, usted es simplemente enchufar valores dados para las variables (ángulos). Sólo asegúrese de usar la fórmula correcta basándose en la información que te dan en la pregunta.
Aquí están los suma y diferencia fórmulas para cosenos:

La suma y diferencia fórmulas de coseno (y seno) pueden hacer más que calcular un valor trig para un ángulo no marcado en el círculo unidad (al menos para los ángulos que son múltiplos de 15 grados). Ellos también se pueden utilizar para encontrar el coseno (y sinusoidal) de la suma o diferencia de dos ángulos en base a la información dada acerca de los dos ángulos. Para este tipo de problemas, se le dará dos ángulos (llamarlos A y B), el seno o coseno de A y B, y el cuadrante (s) en que se encuentran los dos ángulos.
Utilice los siguientes pasos para encontrar el valor exacto de cos (A + B), ya que cos A = -3/5, con A en el cuadrante II del plano de coordenadas, y el pecado B = -7/25, con B en el cuadrante III:
Elija la fórmula adecuada y sustituir la información que usted sabe para determinar la información que falta.

entonces sustituciones resultan en esta ecuación:
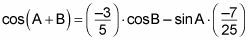
Para continuar más lejos, usted necesita encontrar cos B y el pecado A.
Hacer dibujos que representan los triángulos rectángulos en el cuadrante (s).
Hacer dibujos ayuda a visualizar las piezas faltantes de información.
Es necesario dibujar un triángulo de ángulo A en el cuadrante II y uno para el ángulo B en el cuadrante III. Utilizando la definición de seno como del opp/hyp y el coseno como adj/HYP, esta figura muestra estos triángulos. Observe que el valor de una pata que falta en cada triángulo.
Para encontrar los valores perdidos, utilice el teorema de Pitágoras.
La longitud de la pierna que falta en la figura a es 4, y la longitud de la pierna que falta en la figura b es -24.
Determinar las relaciones trigonométricas que faltan para utilizar en la fórmula suma o diferencia.
Se utiliza la definición de coseno para encontrar que el COS B = -24 / 25 y la definición de seno para encontrar que sen A = 4/5.
Sustituya las relaciones trigonométricas que faltan en la fórmula de suma o diferencia y simplificar.
Ahora tiene esta ecuación:
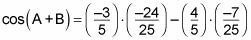
Siga el orden de operaciones para obtener esta respuesta:
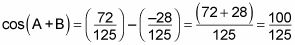
Esta ecuación se simplifica a cos (A + B) = 4/5.
Sobre el autor
 ¿Cómo expresar sumas o diferencias de funciones trigonométricas como productos
¿Cómo expresar sumas o diferencias de funciones trigonométricas como productos Es una buena idea familiarizarse con un conjunto de fórmulas que cambian sumas a los productos. Fórmulas de suma a producto son útiles para ayudarle a encontrar la suma de dos valores trigonométricas que no están en el círculo unitario. Por…
 ¿Cómo encontrar la tangente de la suma o diferencia de ángulos
¿Cómo encontrar la tangente de la suma o diferencia de ángulos Al igual que con seno y coseno, usted puede confiar en fórmulas para encontrar la tangente de una suma o una diferencia de ángulos. La principal diferencia es que no se puede leer tangentes directamente de las coordenadas de los puntos en el…
 Cómo utilizar un ángulo de referencia para encontrar ángulos de soluciones
Cómo utilizar un ángulo de referencia para encontrar ángulos de soluciones En pre-cálculo, a usar funciones trigonométricas para resolver ecuaciones algebraicas. Cuando encuentre el valor del ángulo en una ecuación, que es el ángulo que es una solución a la ecuación, se utiliza que como el ángulo de referencia para…
 Cómo utilizar identidades medio ángulo para evaluar una función trigonométrica
Cómo utilizar identidades medio ángulo para evaluar una función trigonométrica Puede utilizar identidades-medio ángulo para evaluar una función trigonométrica de un ángulo que no está en el círculo unitario utilizando uno que sea. Por ejemplo, 15 grados, que no es en el círculo unitario, es la mitad de 30 grados, que se…
 Asignar valores de la función trigonométrica negativos y positivos por cuadrante
Asignar valores de la función trigonométrica negativos y positivos por cuadrante El primer paso para encontrar el valor de la función trigonométrica de uno de los ángulos que es un múltiplo de 30 o 45 grados es encontrar el ángulo de referencia en el círculo unitario. Cuando el ángulo de referencia viene a ser 0, 30, 45,…
 La comparación de funciones seno y coseno en un gráfico
La comparación de funciones seno y coseno en un gráfico La relación entre el coseno y seno gráficos es que el coseno es el mismo que el sine - solamente se desplaza a la izquierda en 90 grados, o pi-/ 2. La ecuación de trigonometría que representa esta relación esMira las gráficas de las funciones…
 Encuentra identidades trigonométricas opuesto ángulo
Encuentra identidades trigonométricas opuesto ángulo los identidades de ángulo opuesto cambiar las funciones trigonométricas de ángulos negativos a las funciones de ángulos positivos. Ángulos negativos son grandes para describir una situación, pero no son realmente útil cuando se trata de pegar…
 Funciones Gráfico de seno y coseno inversa
Funciones Gráfico de seno y coseno inversa Las gráficas de las funciones trigonométricas inversas son relativamente singularidad por ejemplo, seno inverso y el coseno inversa son un poco brusca y desarticulada. Estos gráficos son importantes debido a su impacto visual. Especialmente en el…
 Cómo utilizar la identidad de ángulo suma, cuando usted no sabe el ángulo
Cómo utilizar la identidad de ángulo suma, cuando usted no sabe el ángulo En algunos problemas de trigonometría, usted no puede saber lo que la medida de un ángulo es, pero usted sabe algo acerca de valores de la función del ángulo. Por ejemplo, suponga que tiene dos ángulos, alfa en el segundo cuadrante de un…
 Cómo utilizar las identidades de resta en un problema trig
Cómo utilizar las identidades de resta en un problema trig Usted puede encontrar valores de la función de los ángulos utilizando identidades ángulo de adición. Y usted tiene más posibilidades de encontrar los valores de la función de los ángulos cuando se utiliza la resta en un problema de…
 Identidades de producto a suma
Identidades de producto a suma Las identidades trigonométricas de producto a suma se parecen mucho. Hay que prestar mucha atención a las diferencias sutiles para que pueda aplicarlas correctamente. A pesar de que el producto se ve bonito y compacto, que no siempre es tan fácil…
 Seno y coseno con el álgebra
Seno y coseno con el álgebra Usted puede aproximar, con bastante precisión, el seno y el coseno de ángulos con un infinito serie, que es la suma de los términos de una secuencia o lista, de los números. Tome en cuenta, sin embargo, que la serie de seno y coseno son exactos…


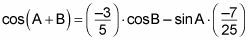
 Hacer dibujos ayuda a visualizar las piezas faltantes de información.
Hacer dibujos ayuda a visualizar las piezas faltantes de información.