Matemáticas normas fundamentales comunes: similitud, triángulos rectángulos, y trigonometría
Las normas esenciales comunes en este grupo se centran principalmente en triángulos. Los estudiantes descubren el concepto de similitud y la escala y explorar cómo estos conceptos se aplican a situaciones del mundo real. La naturaleza única de triángulos también revela algunas verdades matemáticos sobre relaciones que son muy útiles en la resolución de una serie de problemas.
Similitud
En geometría, semejanza se refiere a triángulos que tienen exactamente la misma forma pero difieren en tamaño. Similitud difiere de congruencia, que describe triángulos de tamaño y forma idénticos. El uso de similitud para representar objetos de mayor tamaño es común en campos como la ingeniería y la arquitectura, cuando alguien tiene que representar con precisión el tamaño de ciertos objetos en una escala más pequeña.
Triángulos rectángulos
Los estudiantes trabajan intensamente con triángulos rectángulos (triángulos con un ángulo de 90 grados). Triángulos rectángulos son únicos en que se encuentra la longitud de cualquier lado del triángulo si usted sabe las longitudes de los otros dos lados.
De acuerdo con el teorema de Pitágoras, " el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados, " que se puede expresar como c2 = la2 + b2, donde c es la hipotenusa (el lado más largo del triángulo rectángulo), y la y b son los otros dos lados (más cortos).
Trigonometría
Trigonometría aborda el estudio y el uso de relaciones que implican lados del triángulo y los ángulos. Los estudiantes usan la relaciones seno trigonométrico (pecado), coseno (cos), y tangente (tan) para resolver de piezas (incluyendo un lado que falta o ángulo) de un triángulo rectángulo que faltan:
El uso de razones trigonométricas, se puede determinar la longitud de un lado de un triángulo rectángulo sin conocer las longitudes de los otros dos lados. Puede determinar la longitud desconocida de un lado, dada la longitud de un lado y el ángulo al lado de él. Echa un vistazo por una representación visual de las, y los lados hipotenusa adyacentes opuestas cuando marcada a los efectos de practicar el uso de estas proporciones.
| Usar | Encontrar | Dada |
|---|---|---|
| seno | opuesto | ángulo hipotenusa |
| hipotenusa | ángulo opuesto | |
| ángulo | opuesto y la hipotenusa | |
| coseno | hipotenusa | ángulo adyacente |
| adyacente | ángulo hipotenusa | |
| ángulo | adyacente opuesto | |
| tangente | opuesto | ángulo adyacente |
| adyacente | ángulo opuesto | |
| ángulo | opuesto adyacente |
Desafíe a su hijo a elegir la proporción correcta y encontrar las partes que faltan.
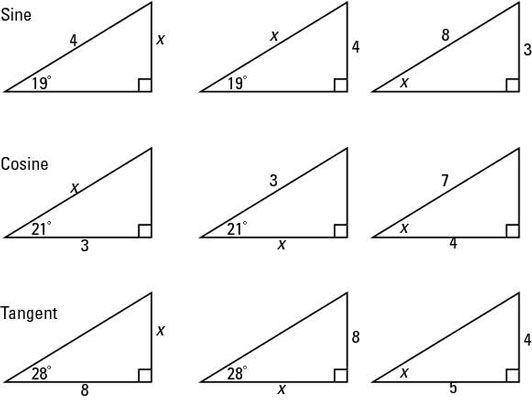
Dibuja triángulos rectángulos de diferentes medidas y dimensiones que tienen las diferentes partes que faltan y que su hijo use las razones trigonométricas de seno, coseno y tangente para encontrar el ángulo que falta o los lados de cada triángulo. Usted ve algunos ejemplos agrupados por coseno, seno y tangente, pero no le dice a su hijo que la relación de usar-desafiarla para averiguarlo.
Por ejemplo, para encontrar X (lado opuesto) del triángulo en la parte superior izquierda, sabiendo que el ángulo es 19 # 176- y la hipotenusa es 4, se utiliza la función seno:
Ser capaz de determinar con precisión el lado que falta o el ángulo de un triángulo rectángulo es importante debido a la frecuencia de triángulos rectángulos en el mundo real, incluyendo objetos cuadrados que se dividen en dos triángulos y ángulos de elevación adecuados.
Razones trigonométricas son aún más útil para encontrar partes que faltan y los ángulos de la no-derecha (oblicuoTriángulos triángulos) - que no cuentan con un ángulo de 90 grados - porque el teorema de Pitágoras trabaja para encontrar solamente faltan lados de triángulos rectángulos.
Puede utilizar la tangente botones (TAN) seno (pecado), coseno (cos), y en la calculadora de su hijo cuando los problemas que requieren el uso de cualquiera de estas razones trigonométricas de trabajo.
-
Alta trig escolar en matemáticas núcleo común -
¿Cómo medir los triángulos -
La aplicación de las fórmulas de suma y diferencia de los cosenos para encontrar el coseno de la suma o diferencia de dos ángulos -
Cómo calcular el seno de un ángulo -
Cómo utilizar un ángulo de referencia para encontrar ángulos de soluciones -
Cómo utilizar SOHCAHTOA para encontrar las funciones trigonométricas de un triángulo rectángulo
¿Cómo trabajar con triángulos 30-60-90 grados Todos los triángulos 30-60-90 grado tienen lados con la misma relación básica. Si nos fijamos en el triángulo 30-60-90 grados en radianes, que se traduce en lo siguiente:En cualquier 30-60-90 triángulo, vea el siguiente:La pierna más corta…
Trabajar con razones trigonométricas en el plano de coordenadas Para poner los ángulos en el plano de coordenadas, esencialmente todo lo que hacemos es mirar las relaciones trigonométricas en términos de X y y valores en vez de frente, adyacente, y hipotenusa. Redefinición de estas proporciones para…
Aplicando el teorema de Pitágoras El teorema de Pitágoras se ha conocido durante al menos 2.500 años. Se utiliza el teorema de Pitágoras cuando se sabe las longitudes de dos lados de un triángulo rectángulo y quiere averiguar la longitud del tercer lado.El teorema de…
La clasificación de tres tipos de triángulos Los triángulos se clasifican según la longitud de sus lados o la medida de sus ángulos. Estas clasificaciones vienen de tres en tres, al igual que los lados y ángulos de sí mismos. Es decir, un triángulo tiene tres lados, y tres términos…
Descubriendo ternas pitagóricas El teorema de Pitágoras es sin duda uno de los teoremas más famosos de toda la matemática. Matemáticos y laicos por igual han estudiado durante siglos, y la gente ha demostrado de muchas maneras diferentes. (Incluso el presidente James Garfield…
Geometría fórmulas y reglas para triángulos Las pirámides de tres ángulos, bidimensionales conocidos como triángulos son uno de los componentes básicos de la geometría (sin embargo de tres picos que sean). Triángulos, por supuesto, tienen sus propias fórmulas para encontrar el área y…
Problemas de la práctica de la geometría con triángulos y polígonos LA polígono es una figura geométrica que tiene al menos tres lados. El triángulo es el polígono más básico. Usted encontrará las siguientes fórmulas y propiedades útiles al responder a las preguntas que implican desigualdades triángulo,…
Libro de Geometría para dummies Si estás estudiando geometría, que se está viendo en todas partes símbolos - símbolos de arcos y ángulos, líneas y triángulos, así como símbolos de las relaciones entre las líneas y ángulos y así sucesivamente. A continuación se…
Cómo resolver problemas de triángulos similares con el teorema de lado divisor Usted puede resolver ciertos problemas de triángulos similares utilizando el Side-divisor teorema. Este teorema afirma que si una línea es paralela a un lado de un triángulo y que interseca los otros dos lados, se divide esos lados…
Cómo utilizar el teorema del ángulo bisectriz El teorema de ángulo-Bisectriz establece que si un rayo biseca un ángulo de un triángulo, a continuación, se divide el lado opuesto en segmentos que son proporcionales a los otros dos lados. La siguiente figura ilustra esto.El teorema de ángulo…
Identificar escaleno, isósceles y triángulos equiláteros Los triángulos se clasifican según la longitud de sus lados o la medida de sus ángulos. Estas clasificaciones vienen de tres en tres, al igual que los lados y ángulos de sí mismos.Las siguientes son las clasificaciones de triángulos basada en…
La identificación de triángulos por sus ángulos Se puede clasificar triángulos por sus ángulos, así como por sus lados. Las clasificaciones basadas en ángulos son como sigue:Triángulo aguda: Un triángulo con tres ángulos agudos (menos de 90 # 176-).Triángulo obtuso: Un triángulo con un…