Trabajar con razones trigonométricas en el plano de coordenadas

Para poner los ángulos en el plano de coordenadas, esencialmente todo lo que hacemos es mirar las relaciones trigonométricas en términos de X y y valores en vez de frente, adyacente, y hipotenusa. Redefinición de estas proporciones para ajustarse al plano de coordenadas (a veces llamado el punto en el plano definición) hace que la visualización de éstos más fácil. Algunos de los ángulos, por ejemplo, son más grandes que 180 grados, pero se puede hacer un triángulo rectángulo con un punto y el X-eje. A continuación, utiliza las nuevas relaciones para encontrar desaparecidos lados de triángulos rectángulos y / o valores de la función trigonométrica de ángulos.

Cuando un punto (X, y) Existe en un plano de coordenadas, se puede calcular todas las funciones trigonométricas del ángulo entre el eje x positivo y el segmento de línea desde el origen hasta el punto (x, y) siguiendo los pasos a continuación (utilice la siguiente figura):

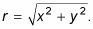
1. Busque el punto en el plano de coordenadas y conectarlo al origen, utilizando una línea recta.

   Digamos, por ejemplo, que se le pide que evaluar todas las seis funciones trigonométricas del ángulo entre el eje x positivo y el segmento de línea que une el origen hasta el punto en el plano (-4, -6). El segmento de línea en movimiento desde este punto hasta el origen es la hipotenusa y ahora se llama el radio r (como se ve en la figura).

2. Dibuje una línea perpendicular que conecta el punto dado a la X-eje, creando un triángulo rectángulo.

   Las patas del triángulo rectángulo son -4 y -6. No deje que los signos negativos asustan usted-las longitudes de los lados siguen siendo 4 y 6. Los signos negativos simplemente revelar la ubicación de ese punto en el plano de coordenadas.

3. Encuentra la longitud de la hipotenusa r mediante el uso de la fórmula de la distancia o el teorema de Pitágoras.

   La distancia que desea buscar es la longitud de r desde el Paso 1. Usando la fórmula de la distancia entre (X, y) Y el origen (0, 0), se obtiene

   

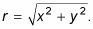
   Recuerde que esta ecuación implica la principal o única raíz positiva, por lo que la hipotenusa de estos triángulos punto-in-the-plano es siempre positivo.

   Para este ejemplo, se obtiene

   

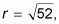
   lo que simplifica a

   

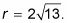
   Checa lo que el triángulo se ve como en la figura.

4. Evalúe los valores de las funciones trigonométricas, usando sus definiciones alternativas.

   Con las etiquetas de la figura, se obtiene la siguiente fórmula:

   

   Sustituye los números del ejemplo de la figura de identificar los valores trigonométricas:

   

5. Simplifique primero:

   

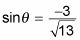
6. Entonces racionalizar el denominador:

   

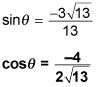
7. Simplifique primero:

   

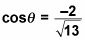
8. Entonces racionalizar:

   

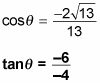
9. Esta respuesta se simplifica a 03.02.

   

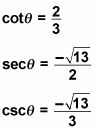
Observe que aún se aplican las reglas de funciones trigonométricas y sus inversas. Por ejemplo, si usted sabe



usted sabe de forma automática



porque son recíprocos.

Cuando el punto de que te dan es un punto en uno de los ejes, aún se pueden encontrar todos los valores de la función trigonométrica del ángulo formado con lo positivo X-eje. Por ejemplo, si el punto está en el X-eje, la pata adyacente al ángulo theta y el radio tienen el mismo valor absoluto (porque el coseno puede ser negativo, pero el radio no se puede). Por lo tanto, si el punto está en el positivo X-eje, el coseno de theta es 1 y el seno de theta es 0- si el punto está en el negativo X-eje, el coseno de theta es -1 y el seno de theta todavía será 0. Del mismo modo, si el punto está en el y-eje, el cateto opuesto al ángulo theta y el radio son del mismo valor absoluto. Por lo tanto, si el punto está en el positivo y-eje, el seno de theta será 1, y el coseno será 0- si el punto está en el negativo y-eje, el seno de theta será -1 y el coseno seguirá siendo 0.