Cómo trazar los grandes ángulos de todo el círculo unidad

Usted puede tomar los ángulos unidad de círculo y los triángulos rectángulos especiales y ponerlos juntos para crear un pequeño paquete: el círculo unidad completa. Usted crea triángulos especiales en el círculo unidad uno a la vez, porque son todos los puntos en el plano de coordenadas.

Independientemente de cuánto tiempo los lados se que forman un ángulo particular en un triángulo, los valores de la función de trigonometría para ese ángulo específico son siempre los mismos. Por lo tanto, los matemáticos se redujeron todos los lados de triángulos rectángulos para que todos habían encajan en el círculo unitario.

La hipotenusa de todo triángulo en un círculo unidad es siempre 1, por lo que los cálculos que implican los triángulos mucho más fácil de calcular. Debido a la circunferencia unidad, puede dibujar alguna ángulo con alguna medición, y todos los triángulos rectángulos con el mismo ángulo de referencia son del mismo tamaño.

Comenzando en el cuadrante I, mira en un ángulo marcado 30 grados en el círculo unidad (que se muestra en la figura anterior):

1. Dibuja el ángulo y conectarlo al origen, utilizando una línea recta.

   El lado del terminal de un ángulo de 30 grados debe estar en el primer cuadrante, y el tamaño del ángulo debe ser bastante pequeño. De hecho, debería ser de un tercio de la distancia entre 0 grados y 90 grados.

2. Dibuje una línea perpendicular que conecta el punto donde el rayo se detiene a la X-eje, creando un triángulo rectángulo.

   Hipotenusa del triángulo es el radio de la unidad de círculo- una de sus patas es en el X-eje- y la otra pata es paralela a la y-eje. Usted puede ver lo que este triángulo 30-60-90 grados se ve como en la figura.

3. Encuentra la longitud de la hipotenusa.

   El radio de la circunferencia unidad es siempre 1, lo que significa la hipotenusa del triángulo es también 1.

4. Encuentra las longitudes de los otros lados.

   Para encontrar los otros dos lados, a encontrar la pata corta primero dividiendo por 2, lo que le da medio. Para encontrar la pierna larga, multiplicar 2.1 por

   

5. Identificar el punto en el círculo unitario.

   El círculo unidad está en el plano de coordenadas, centrado en el origen. Así que cada uno de los puntos de la circunferencia unidad tiene coordenadas únicas. Ahora puede nombrar el punto a 30 grados sobre el círculo:

   

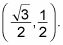
Después de pasar por estos pasos, usted puede encontrar fácilmente los puntos de otros ángulos en el círculo unidad también. Por ejemplo:

• Mira el punto en el círculo marcado 45 grados. Puede dibujar un triángulo de ella, utilizando los pasos 1 y 2. Su hipotenusa es todavía 1, el radio del círculo unitario. Para encontrar la longitud de los catetos de un triángulo 45-45-90 grados, se divide la hipotenusa por

  

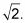
  A continuación, racionalizar el denominador para obtener

  

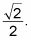
  Ahora puede llamar a este punto en el círculo

  

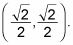
• Moverse hacia la izquierda al ángulo de 60 grados, se puede crear un triángulo con los pasos 1 y 2. Si se mira de cerca, te darás cuenta de que este es un triángulo 30-60-90 con el ángulo de 30 grados en la parte superior, por lo que el lado corto es el lado en el X-eje. Eso hace que el punto a 60 grados

  

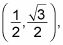
  y porque el radio es 1, (1 dividir por 2 para obtener la longitud del lado corto como media). Luego multiplique por medio

  

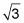
  para obtener la longitud del lado largo como

  

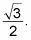
Cuadrantes II a IV en el plano de coordenadas son sólo imágenes especulares el primer cuadrante. Sin embargo, los signos son diferentes porque los puntos sobre el círculo unitario se encuentran en diferentes lugares del plano:

• En el cuadrante I, tanto X y y los valores son positivos.

• En el cuadrante II, X es negativo y y es positivo.

• En el cuadrante III, tanto X y y son negativos.

• En el cuadrante IV, X es positivo y y es negativo.

  
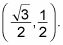  El círculo unidad de conjunto.

La buena noticia es que usted nunca tiene que memorizar todo el círculo unidad. Usted puede simplemente aplicar los fundamentos de lo que sabe sobre triángulos rectángulos y el círculo unidad! La figura anterior muestra toda la empanada de pizza del círculo unitario.