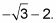¿Cómo encontrar la tangente de la suma o diferencia de ángulos
Al igual que con seno y coseno, usted puede confiar en fórmulas para encontrar la tangente de una suma o una diferencia de ángulos. La principal diferencia es que no se puede leer tangentes directamente de las coordenadas de los puntos en el círculo unitario, como usted puede con seno y coseno, ya que cada punto representa
Toda esperanza no se pierde, sin embargo, debido a que la tangente de un ángulo # 952- se define como el pecado # 952- / cos # 952-. Debido a que el seno del ángulo es la y-coordinar y el coseno es la X-coordinar, usted puede expresar la tangente en términos de X y y en el círculo unidad, y/X.
Estas son las fórmulas que necesita para encontrar la tangente de una suma o diferencia de ángulos:
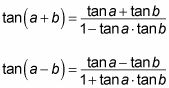
Usted debe memorizar estas fórmulas poco dulces, porque entonces usted no tendrá que utilizar los suma y diferencia fórmulas de seno y coseno en medio de un problema de la tangente, ahorrándole tiempo en el largo plazo. Si decide no de memorizar estas dos fórmulas, puede derivar de ellos recordando estas ecuaciones:
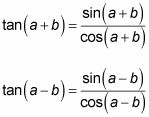
La suma y diferencia fórmulas de trabajo tangente de manera similar a los de las fórmulas de seno y coseno. Puede utilizar las fórmulas para resolver una variedad de problemas, tales como la forma de encontrar la tangente de un ángulo que no está marcado en el círculo unitario. Usted puede hacerlo, siempre y cuando el ángulo se puede escribir como la suma o diferencia de ángulos especiales.
Por ejemplo, para encontrar el valor exacto de bronceado 105 grados, siga estos pasos (tenga en cuenta que el ángulo de 105 grados es en el cuadrante II):
Vuelva a escribir el ángulo dado, utilizando la información de derecho especial; ángulos del triángulo.
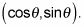El círculo unidad enteraConsulte el círculo unitario, señalando que se construye a partir de los triángulos rectángulos especiales, para encontrar una combinación de ángulos que se suman o se restan para obtener 105 grados. Usted puede elegir entre 240 grados - 135 grados, 330 grados - 225 grados, y así sucesivamente. Este ejemplo utiliza 60 grados + 45 grados.
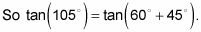
Debido a que el ángulo se reescribe con la adición, es necesario utilizar la fórmula suma por la tangente.
Enchufe la información que usted sabe en la fórmula apropiada.
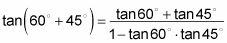
Use el círculo unitario para buscar los valores de seno y coseno que usted necesita.
Para encontrar bronceado 60 # 186-, debe localizar 60 # 176- en el círculo unitario y luego usar el punto correspondiente en el círculo unitario para obtener los valores de seno y coseno para calcular la tangente:
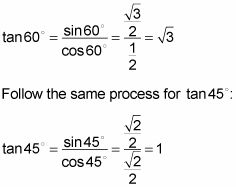
Sustituye los valores trigonométricas desde el paso 3 en la fórmula.
Este paso le da
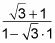
lo que simplifica a
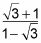
Racionalizar el denominador.
No se puede dejar la raíz cuadrada en el denominador de una fracción. Debido a que el denominador es un binomio (la suma o diferencia de dos términos), se debe multiplicar el numerador y el denominador por el conjugado del denominador. El conjugado de la + b es la - b, y viceversa.
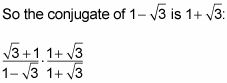
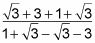
Simplifica la fracción racionalizado para encontrar el valor exacto de la tangente.
Combine los términos semejantes para conseguir
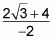
Asegúrese de simplificar plenamente esta fracción para obtener
-
La aplicación de las fórmulas de suma y diferencia de los cosenos para encontrar el coseno de la suma o diferencia de dos ángulos -
Cómo aplicar las fórmulas de suma y diferencia de coseno de trig pruebas -
Cómo aplicar las fórmulas de suma y diferencia de tangente a trig pruebas -
Cómo calcular el seno de ángulos especiales en grados -
Cómo calcular el seno de ángulos especiales en radianes -
Cómo calcular los valores para las seis funciones trigonométricas
¿Cómo expresar sumas o diferencias de funciones trigonométricas como productos Es una buena idea familiarizarse con un conjunto de fórmulas que cambian sumas a los productos. Fórmulas de suma a producto son útiles para ayudarle a encontrar la suma de dos valores trigonométricas que no están en el círculo unitario. Por…
Cómo graficar una función tangente La función tangente tiene una gráfica de los padres al igual que cualquier otra función. Utilizando la gráfica de esta función, se puede hacer el mismo tipo de transformación que se aplica a la gráfica de los padres de cualquier función. La…
Cómo graficar seno, coseno y tangente Así, es necesario graficar un seno, coseno, tangente o función. Seno, coseno y tangente - y sus inversos, cosecante, secante y cotangente - son periódico funciones, lo que significa que sus gráficos contienen una forma básica que se repite una…
Cómo utilizar identidades medio ángulo para evaluar una función trigonométrica Puede utilizar identidades-medio ángulo para evaluar una función trigonométrica de un ángulo que no está en el círculo unitario utilizando uno que sea. Por ejemplo, 15 grados, que no es en el círculo unitario, es la mitad de 30 grados, que se…
Cómo determinar la medida de un ángulo cuyo vértice se encuentra fuera de un círculo Un ángulo que cruza un círculo puede tener su vértice en el interior, sobre o fuera del círculo. Este artículo aborda los tres tipos de ángulos que tienen sus vértices fuera de un círculo: ángulos secante-secantes, ángulos…
Tratar con identidades medio-ángulo que involucran radicales Mediante la adición, sustracción, o duplicando medidas de los ángulos, se puede encontrar gran cantidad de valores exactos de las funciones trigonométricas. Por ejemplo, puede utilizar la identidad de medio ángulo cuando el valor exacto de la…
Encuentra identidades trigonométricas opuesto ángulo los identidades de ángulo opuesto cambiar las funciones trigonométricas de ángulos negativos a las funciones de ángulos positivos. Ángulos negativos son grandes para describir una situación, pero no son realmente útil cuando se trata de pegar…
Cómo calcular las funciones trigonométricas de ángulos usando el círculo unitario Cálculo de funciones trigonométricas de ángulos dentro de un círculo unidad es muy fácil. La figura muestra un círculo unitario, que tiene la ecuación X2 + y2 = 1, junto con algunos puntos de la circunferencia y sus coordenadas.El uso de los…
¿Cómo encontrar identidades medio-ángulo para tangente La media de ángulo trig identidad para tangente tiene dos versiones. En lugar de que esto sea una molestia, que tiene más de una opción es realmente bastante agradable, porque se puede elegir la versión que mejor se adapte a su situación. Las…
Encontrar la función de la trigonometría de un ángulo en un círculo unitario Puede determinar las funciones trigonométricas de cualquier ángulo que se encuentran en el círculo unitario - cualquiera que se grafican en posición estándar (es decir, el vértice del ángulo está en el origen, y el lado inicial se encuentra…
Cómo utilizar la identidad de ángulo suma, cuando usted no sabe el ángulo En algunos problemas de trigonometría, usted no puede saber lo que la medida de un ángulo es, pero usted sabe algo acerca de valores de la función del ángulo. Por ejemplo, suponga que tiene dos ángulos, alfa en el segundo cuadrante de un…
Cómo utilizar las identidades de resta en un problema trig Usted puede encontrar valores de la función de los ángulos utilizando identidades ángulo de adición. Y usted tiene más posibilidades de encontrar los valores de la función de los ángulos cuando se utiliza la resta en un problema de…