Encuentra identidades trigonométricas opuesto ángulo

los identidades de ángulo opuesto cambiar las funciones trigonométricas de ángulos negativos a las funciones de ángulos positivos. Ángulos negativos son grandes para describir una situación, pero no son realmente útil cuando se trata de pegar en una función trigonométrica y cálculo de dicho valor. Así, por ejemplo, se puede reescribir el seno de -30 grados como el seno de 30 grados, poniendo un signo negativo delante de la función:

La identidad funciona de forma diferente para diferentes funciones, sin embargo. En primer lugar, considerar las identidades, y luego averiguar cómo llegaron a ser.

Las identidades de distinto ángulo para las tres funciones más básicas son

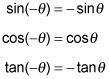
La regla para el seno y la tangente de un ángulo negativo casi parece intuitivo. Pero, ¿qué pasa con el coseno? ¿Cómo puede el coseno de un ángulo negativo ser el mismo que el coseno del ángulo positivo correspondiente? Así es como funciona.

Las funciones de ángulos con sus lados terminales en los diferentes cuadrantes tienen diferentes signos. Sine, por ejemplo, es positivo cuando el lado terminal del ángulo se encuentra en el primer y segundo cuadrantes, mientras que el coseno es positivo en el primer y cuarto cuadrantes. Además, los ángulos positivos van en sentido antihorario desde el positivo X-eje, y los ángulos negativos van en sentido horario.

Con estos puntos en mente, eche un vistazo a la figura anterior, lo que muestra un ángulo de -45 grados y un ángulo de 45 grados.

En primer lugar, tenga en cuenta el ángulo de -45 grados. Este ángulo tiene su lado terminal en el cuarto cuadrante, por lo que su seno es negativo. Un ángulo de 45 grados, por otro lado, tiene un sine positivo, por lo

En la llanura Inglés, el seno de un ángulo negativo es el valor opuesto de la del ángulo positivo con la misma medida.

Ahora a la función coseno. A la luz de señal del coseno con respecto al plano de coordenadas, usted sabe que un ángulo de -45 grados tiene un coseno positivo. Lo mismo ocurre con su contraparte, el ángulo de 45 grados, por lo que

Así que ya ves, el coseno de un ángulo negativo es la misma que la del ángulo positivo con la misma medida.

A continuación, pruebe la identidad de otro ángulo, un ángulo negativo con su lado terminal en el tercer cuadrante. La figura anterior muestra un ángulo negativo con la medida de -120 grados y su ángulo positivo correspondiente, 120 grados.

El ángulo de -120 grados tiene su lado terminal en el tercer cuadrante, por lo tanto en su seno y coseno son negativos. Su contraparte, el ángulo de medición de 120 grados, tiene su lado terminal en el segundo cuadrante, donde el seno es positivo y el coseno es negativo. Así el seno de -120 grados es el opuesto de la sinusoidal de 120 grados, y el coseno de -120 grados es el mismo que el coseno de 120 grados. En la notación trigonométrica, se ve así:

Cuando se aplica la identidad de distinto ángulo a la tangente de un ángulo de 120 grados (que viene a ser negativo), se obtiene que el contrario de un negativo es un positivo. Sorpresa sorpresa. Por lo tanto, la aplicación de la identidad, lo contrario hace la tangente positiva, que es lo que usted consigue cuando usted toma la tangente de 120 grados, en el lado del terminal se encuentra en el tercer cuadrante, y es, por tanto, positivo.