¿Cómo trabajar con funciones trigonométricas inversas
La forma más fácil de trabajar con funciones trigonométricas inversas es tener una práctica tabla con los valores exactos de las funciones. Cuando ángulos distintos de los más comunes o populares están involucrados, puede utilizar una tabla o salir de su calculadora científica práctico-excelente.
Cuando se trabaja con la trigonometría mucho, pronto tiene los ángulos básicos y sus valores de función memorizados. Usted también sabe que el seno y su recíproco son positivos en QI y QII- el coseno y su recíproco son positivos en QI y QIV- y la tangente y su recíproco son positivos en QI y QIII. Armado con el conceptos básicos, se puede llegar a valores de la función en lugar de forma rápida y eficiente - sin recurrir a trazar o calculadora.
Este primer ejemplo se utiliza el valor exacto de un gráfico (o desde la memoria). Encontrar
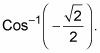
Determinar el ángulo de referencia que necesita utilizando el valor absoluto de la entrada.
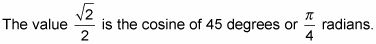
Utilice la señal de la entrada para determinar el cuadrante correcto.
Porque
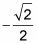
es negativo, y de los dos cuadrantes de la gama, el coseno es negativo en QII, la respuesta es un ángulo en QII cuyo ángulo de referencia es de 45 grados.
Determine la medida del ángulo correcto.
El ángulo en posición estándar en QII cuya referencia ángulo es de 45 grados es
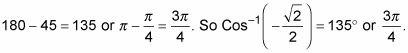
El siguiente ejemplo involucra cotangente inversa. Encontrar
Determinar el ángulo de referencia que usted necesita.
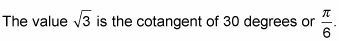
Utilice la señal de la entrada para determinar el cuadrante correcto.
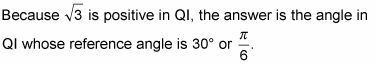
Determine la medida del ángulo correcto.
Todos los ángulos en QI son las mismas que sus ángulos de referencia, por lo
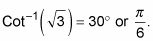
Los problemas que encuentre no siempre implicarán números agradables desde los ángulos más comunes. Cuando te enfrentas a un pequeño valor decimal desagradable, puede que tenga que utilizar una tabla. En el siguiente ejemplo, usted comienza con un valor decimal y una respuesta a la más cerca grado es la respuesta adecuada. El decimal en el siguiente ejemplo se completa con tres decimales. Para estos problemas, a encontrar la respuesta más cercana.
Encuentra Arctan (-3.732).
Determinar el ángulo de referencia que usted necesita.
Mediante el uso de una tabla, se puede ver que el valor 3.732 corresponde a la tangente de un ángulo de 75 grados. Este ángulo es el más cercano en grados enteros de tener una tangente de 3,732.
Utilice la señal de la entrada para determinar el cuadrante correcto.
Debido -3,732 es negativo, la respuesta es un ángulo en QIV cuyo ángulo de referencia es de 75 grados.
Determine la medida del ángulo correcto.
En QIV, un ángulo de referencia de 75 grados tiene una medida de cualquiera de -75 grados o su equivalente positivo (mismo lado terminal), 285 grados. Así Arctan (-3.732) = tan-1(-3.732) = -75 # 176- o 285 # 176-.
-
Cómo calcular un ángulo utilizando funciones trigonométricas inversas -
Cómo dibujar ángulos poco comunes -
Cómo utilizar identidades medio ángulo para evaluar una función trigonométrica -
Cómo determinar la medida de un ángulo cuyo vértice se encuentra fuera de un círculo -
Asignar valores de la función trigonométrica negativos y positivos por cuadrante -
Asignar funciones trigonométricas negativos y positivos por cuadrante
Tratar con identidades medio-ángulo que involucran radicales Mediante la adición, sustracción, o duplicando medidas de los ángulos, se puede encontrar gran cantidad de valores exactos de las funciones trigonométricas. Por ejemplo, puede utilizar la identidad de medio ángulo cuando el valor exacto de la…
Encuentra identidades trigonométricas opuesto ángulo los identidades de ángulo opuesto cambiar las funciones trigonométricas de ángulos negativos a las funciones de ángulos positivos. Ángulos negativos son grandes para describir una situación, pero no son realmente útil cuando se trata de pegar…
Ángulos gráfico en una posición estándar Navegantes, agrimensores, carpinteros y todos utilizan las mismas medidas de los ángulos, pero los ángulos comienzan en diferentes posiciones o lugares. En trigonometría y la mayoría de las otras disciplinas matemáticas, dibujar ángulos en una…
Cómo calcular los ángulos de referencia en grados Despejando el ángulo de referencia en grados es mucho más fácil que tratar de determinar una función trigonométrica del ángulo original. Para calcular la medida (en grados) del ángulo de referencia para cualquier ángulo theta dado, utilizar…
Cómo calcular los ángulos de referencia en radianes Despejando el ángulo de referencia en radianes es mucho más fácil que tratar de determinar una función trigonométrica del ángulo original. Para calcular la medida (en radianes) del ángulo de referencia para cualquier ángulo theta dado,…
Encontrar la función de la trigonometría de un ángulo en un círculo unitario Puede determinar las funciones trigonométricas de cualquier ángulo que se encuentran en el círculo unitario - cualquiera que se grafican en posición estándar (es decir, el vértice del ángulo está en el origen, y el lado inicial se encuentra…
Cómo localizar ángulos de referencia Cada uno de los ángulos en un círculo unidad tiene un ángulo de referencia, que es siempre un ángulo agudo positivo (excepto los ángulos que ya son positivas y aguda). Al identificar el ángulo de referencia, se puede determinar los valores de…
Cómo cambiar el nombre de los ángulos coterminales Cualquier ángulo puede tener muchas, muchas descripciones en términos de medidas de ángulos, ya que un ángulo es equivalente a sus ángulos coterminales. Las medidas de los ángulos positivos utilizados con mayor frecuencia son los que miden…
¿Cómo resolver funciones trigonométricas inversas con ángulos poco comunes Cuando se trabaja con funciones trigonométricas inversas, siempre es más conveniente cuando los números que está trabajando son los resultados de la aplicación de una de las funciones trigonométricas a una medida de ángulo común. Cuando el…
Cómo utilizar identidades medio ángulo para encontrar el seno de un ángulo Mediante la adición, sustracción, o duplicando medidas de los ángulos, se puede encontrar gran cantidad de valores exactos de las funciones trigonométricas utilizando las funciones de ángulos que ya conoce. Por ejemplo, a pesar de que se puede…
Cómo utilizar la identidad de ángulo suma, cuando usted no sabe el ángulo En algunos problemas de trigonometría, usted no puede saber lo que la medida de un ángulo es, pero usted sabe algo acerca de valores de la función del ángulo. Por ejemplo, suponga que tiene dos ángulos, alfa en el segundo cuadrante de un…
Cómo utilizar la identidad de doble ángulo para el seno La fórmula de doble ángulo para el seno proviene del uso de la identidad trigonométrica para el seno de una suma, el pecado (alfa + beta-) = sinalpha-cosbeta- +-cosalpha sinbeta-. Si alfa = beta-, entonces se puede sustituir beta- con alfa en la…