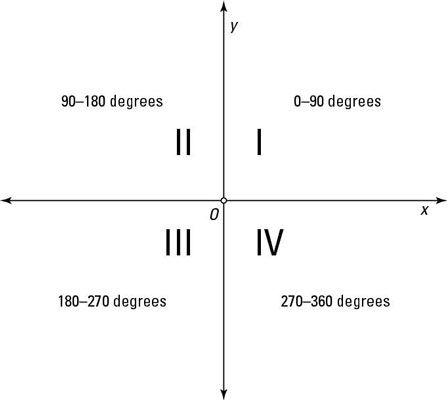
Ángulos gráfico en una posición estándar
Navegantes, agrimensores, carpinteros y todos utilizan las mismas medidas de los ángulos, pero los ángulos comienzan en diferentes posiciones o lugares. En trigonometría y la mayoría de las otras disciplinas matemáticas, dibujar ángulos en una norma, la posición universal, por lo que los matemáticos de todo el mundo están llamando y hablando de la misma cosa.
Posicionamiento lados inicial y terminal
Un ángulo en posición estándar tiene su vértice en el origen del plano de coordenadas. Su inicial ray (lado de partida) se encuentra a lo largo del positiva X-eje. Su Terminal rayo (lado final) se mueve en sentido antihorario desde el lado inicial.
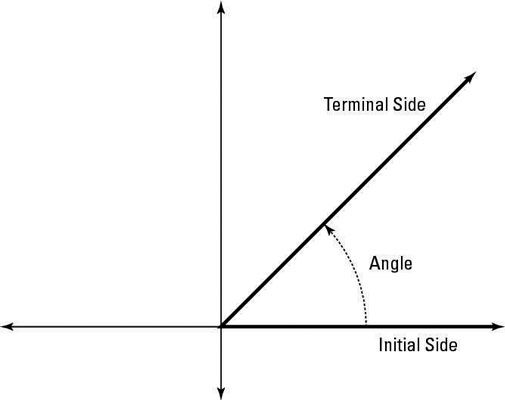
Si los rayos mueve terminales hacia la derecha en vez de la izquierda, a continuación, la medida es un valor negativo. A menudo se nombra ángulos en posición estándar con una letra griega.
Las longitudes de los rayos que crean el ángulo no tienen nada que ver con el tamaño del ángulo. Puede ampliar los rayos siempre y cuando usted los necesita para ser, y la medida del ángulo no va a cambiar. Sólo la posición del rayo terminal determina el ángulo.
Medición por cuadrantes
Ángulos en la posición estándar se utilizan en el cálculo, geometría, trigonometría, y otros temas de matemáticas como base para la discusión. Ser capaz de reconocer un ángulo particular por el cuadrante de su lado del terminal se encuentra en y, a la inversa, para saber qué ángulos tienen sus lados terminales en un cuadrante particular es útil cuando se trabaja en estas áreas.
Los ángulos en posición estándar que miden entre 0 y 90 grados tienen sus lados terminales en el cuadrante I. Los ángulos que miden entre 90 y 180 grados tienen sus lados terminales en el Cuadrante II. Los ángulos que miden entre 180 y 270 tienen sus lados terminales en el cuadrante III, y los que miden entre 270 y 360 tienen sus lados terminales en el cuadrante IV.
Los ángulos que miden exactamente 90, 180, 270 y 360 grados no tienen un lado del terminal que se encuentra en un cuadrante, y están referidos como cuadranteotros ángulos.
Asignar valores de la función trigonométrica negativos y positivos por cuadrante El primer paso para encontrar el valor de la función trigonométrica de uno de los ángulos que es un múltiplo de 30 o 45 grados es encontrar el ángulo de referencia en el círculo unitario. Cuando el ángulo de referencia viene a ser 0, 30, 45,…
Triángulos trigonométricas básicas Todo por su cuenta, los ángulos son sin duda muy emocionante. Pero los puso en un triángulo, y usted tiene la guinda del pastel. Triángulos son una de las figuras geométricas estudiadas con más frecuencia. Los ángulos que forman el triángulo…
Ángulos trigonométricos básicos Cuando dos líneas, segmentos, o rayos táctil o se cruzan entre sí, forman un ángulo o ángulos. En el caso de dos líneas que se cruzan, el resultado es cuatro ángulos diferentes. Cuando dos segmentos se cruzan, pueden formar uno, dos, o cuatro…
Encuentra identidades trigonométricas opuesto ángulo los identidades de ángulo opuesto cambiar las funciones trigonométricas de ángulos negativos a las funciones de ángulos positivos. Ángulos negativos son grandes para describir una situación, pero no son realmente útil cuando se trata de pegar…
Cómo calcular los ángulos de referencia en grados Despejando el ángulo de referencia en grados es mucho más fácil que tratar de determinar una función trigonométrica del ángulo original. Para calcular la medida (en grados) del ángulo de referencia para cualquier ángulo theta dado, utilizar…
Cómo calcular los ángulos de referencia en radianes Despejando el ángulo de referencia en radianes es mucho más fácil que tratar de determinar una función trigonométrica del ángulo original. Para calcular la medida (en radianes) del ángulo de referencia para cualquier ángulo theta dado,…
Encontrar la función de la trigonometría de un ángulo en un círculo unitario Puede determinar las funciones trigonométricas de cualquier ángulo que se encuentran en el círculo unitario - cualquiera que se grafican en posición estándar (es decir, el vértice del ángulo está en el origen, y el lado inicial se encuentra…
Cómo localizar ángulos de referencia Cada uno de los ángulos en un círculo unidad tiene un ángulo de referencia, que es siempre un ángulo agudo positivo (excepto los ángulos que ya son positivas y aguda). Al identificar el ángulo de referencia, se puede determinar los valores de…
Cómo cambiar el nombre de los ángulos coterminales Cualquier ángulo puede tener muchas, muchas descripciones en términos de medidas de ángulos, ya que un ángulo es equivalente a sus ángulos coterminales. Las medidas de los ángulos positivos utilizados con mayor frecuencia son los que miden…
Cómo utilizar la identidad de ángulo suma, cuando usted no sabe el ángulo En algunos problemas de trigonometría, usted no puede saber lo que la medida de un ángulo es, pero usted sabe algo acerca de valores de la función del ángulo. Por ejemplo, suponga que tiene dos ángulos, alfa en el segundo cuadrante de un…
¿Cómo trabajar con funciones trigonométricas inversas La forma más fácil de trabajar con funciones trigonométricas inversas es tener una práctica tabla con los valores exactos de las funciones. Cuando ángulos distintos de los más comunes o populares están involucrados, puede utilizar una tabla o…
Identificar ángulos coterminales Dos ángulos son coterminal si tienen el mismo lado terminal. Usted tiene un número infinito de formas de dar una medida de ángulo de un rayo terminal en particular. A veces, el uso de un ángulo negativo en lugar de un ángulo positivo es más…