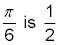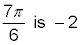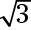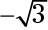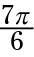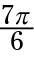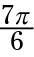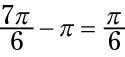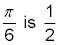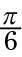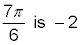Encontrar la función de la trigonometría de un ángulo en un círculo unitario
Puede determinar las funciones trigonométricas de cualquier ángulo que se encuentran en el círculo unitario - cualquiera que se grafican en posición estándar (es decir, el vértice del ángulo está en el origen, y el lado inicial se encuentra a lo largo del positiva X-eje). Utiliza las reglas para los ángulos de referencia, los valores de las funciones de ciertos ángulos agudos, y la regla de los signos de las funciones.
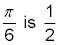
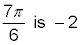
Ahora, armado con toda la información necesaria, encontrar la tangente de 300 grados.
Encuentra el ángulo de referencia.
Usando la tabla superior, se puede ver que un ángulo de 300 grados tiene su lado terminal en el cuarto cuadrante, por lo que encontrar el ángulo de referencia restando 300 de 360. Por lo tanto, la medida del ángulo de referencia es de 60 grados.
Encontrar el valor numérico de la tangente.
Usando la tabla media, se ve que el valor numérico de la tangente de 60 grados es
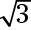
Encuentra el signo de la tangente.
Debido a un ángulo de 300 grados es en el cuarto cuadrante, y ángulos en ese cuadrante tienen tangentes negativos (consulte la sección anterior), la tangente de 300 grados es
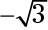
Para probar su mano en el trabajo con radianes, encontrar la cosecante de
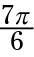
Encuentra el ángulo de referencia.
Para utilizar el gráfico superior, es necesario determinar la equivalencia grados para un ángulo de medición
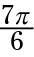
Utilizando la fórmula para convertir de radianes a grados, se obtiene que
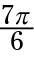
es equivalente a 210 # 176-. Este ángulo está en el tercer cuadrante, así, que se remonta a radianes, a encontrar el ángulo de referencia restando # 960- desde
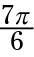
Resultando en
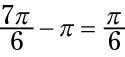
Encontrar el valor numérico de la cosecante.
En el gráfico de media 2, no aparece la cosecante. Sin embargo, el recíproco de la cosecant es sinusoidal. Así que encontrar el valor del seno, y utilizar su recíproco. El seno de
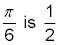
lo que significa que la cosecante de
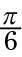
es 2 (el recíproco).
Encuentra el signo de la cosecante.
En el tercer cuadrante, la cosecante de un ángulo es negativo, por lo que la cosecante de
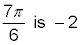
Sobre el autor
 Una tabla rápida para las tres funciones trigonométricas recíprocas
Una tabla rápida para las tres funciones trigonométricas recíprocas Usted sabe que las funciones recíprocas tienen valores que son recíprocos, o voltea, de los valores de sus respectivas funciones. El recíproco de seno es cosecante, por lo que cada valor de la función para la cosecante es el recíproco del seno…
 Asignar valores de la función trigonométrica negativos y positivos por cuadrante
Asignar valores de la función trigonométrica negativos y positivos por cuadrante El primer paso para encontrar el valor de la función trigonométrica de uno de los ángulos que es un múltiplo de 30 o 45 grados es encontrar el ángulo de referencia en el círculo unitario. Cuando el ángulo de referencia viene a ser 0, 30, 45,…
 Asignar funciones trigonométricas negativos y positivos por cuadrante
Asignar funciones trigonométricas negativos y positivos por cuadrante Los valores de seno para 30, 150, 210 y 330 grados son 1/2, 1/2, -1/2 y -1/2, respectivamente. Todos estos múltiplos de 30 grados tienen un pecado cuyo valor absoluto del medio. La siguiente regla y figura ayudarle a determinar si un valor…
 Funciones trigonométricas secantes gama de Dominio y cosecante y
Funciones trigonométricas secantes gama de Dominio y cosecante y Las funciones cosecante y secante están estrechamente ligados a seno y coseno, porque son los respectivos recíprocos. En referencia al plano de coordenadas, cosecante es r/y, y secante es r/X. El valor de r es la longitud de la hipotenusa de un…
 Encuentra identidades trigonométricas opuesto ángulo
Encuentra identidades trigonométricas opuesto ángulo los identidades de ángulo opuesto cambiar las funciones trigonométricas de ángulos negativos a las funciones de ángulos positivos. Ángulos negativos son grandes para describir una situación, pero no son realmente útil cuando se trata de pegar…
 Ángulos gráfico en una posición estándar
Ángulos gráfico en una posición estándar Navegantes, agrimensores, carpinteros y todos utilizan las mismas medidas de los ángulos, pero los ángulos comienzan en diferentes posiciones o lugares. En trigonometría y la mayoría de las otras disciplinas matemáticas, dibujar ángulos en una…
 Cómo calcular las funciones trigonométricas de ángulos usando el círculo unitario
Cómo calcular las funciones trigonométricas de ángulos usando el círculo unitario Cálculo de funciones trigonométricas de ángulos dentro de un círculo unidad es muy fácil. La figura muestra un círculo unitario, que tiene la ecuación X2 + y2 = 1, junto con algunos puntos de la circunferencia y sus coordenadas.El uso de los…
 Cómo calcular los ángulos de referencia en grados
Cómo calcular los ángulos de referencia en grados Despejando el ángulo de referencia en grados es mucho más fácil que tratar de determinar una función trigonométrica del ángulo original. Para calcular la medida (en grados) del ángulo de referencia para cualquier ángulo theta dado, utilizar…
 Cómo calcular los ángulos de referencia en radianes
Cómo calcular los ángulos de referencia en radianes Despejando el ángulo de referencia en radianes es mucho más fácil que tratar de determinar una función trigonométrica del ángulo original. Para calcular la medida (en radianes) del ángulo de referencia para cualquier ángulo theta dado,…
 Cómo localizar ángulos de referencia
Cómo localizar ángulos de referencia Cada uno de los ángulos en un círculo unidad tiene un ángulo de referencia, que es siempre un ángulo agudo positivo (excepto los ángulos que ya son positivas y aguda). Al identificar el ángulo de referencia, se puede determinar los valores de…
 Cómo utilizar identidades medio ángulo para encontrar el seno de un ángulo
Cómo utilizar identidades medio ángulo para encontrar el seno de un ángulo Mediante la adición, sustracción, o duplicando medidas de los ángulos, se puede encontrar gran cantidad de valores exactos de las funciones trigonométricas utilizando las funciones de ángulos que ya conoce. Por ejemplo, a pesar de que se puede…
 Cómo utilizar la identidad de ángulo suma, cuando usted no sabe el ángulo
Cómo utilizar la identidad de ángulo suma, cuando usted no sabe el ángulo En algunos problemas de trigonometría, usted no puede saber lo que la medida de un ángulo es, pero usted sabe algo acerca de valores de la función del ángulo. Por ejemplo, suponga que tiene dos ángulos, alfa en el segundo cuadrante de un…