Cómo calcular los valores para las seis funciones trigonométricas
En pre-cálculo, es necesario evaluar las seis funciones trigonométricas - seno, coseno, tangente, cosecante, secante y cotangente - para un solo ángulo en el círculo unitario. Para cada ángulo en la circunferencia unidad, otros tres ángulos tienen valores de la función trigonométrica similares. La única diferencia es que los signos de estos valores son opuestas, dependiendo de qué cuadrante del ángulo es. A veces el ángulo no será en el círculo unitario y tendrás que usar la calculadora.
Si usted no tiene el círculo unidad a su disposición (si usted está tomando un examen, por ejemplo), puede dibujar una imagen y encontrar los valores que necesita el camino largo.
La definición de punto en el plano del coseno en un triángulo rectángulo es
Debido a que la hipotenusa r es siempre 1 en la unidad de círculo, el X valor es el valor del coseno. Y si usted recuerda la definición alternativa de seno,
te darás cuenta de que el y valor es el valor del seno. Por lo tanto, cualquier punto en cualquier lugar en el círculo unitario es siempre
Hable acerca de poner todas las piezas juntas!
Por orden alfabético, X viene antes y y c viene antes s (coseno viene antes de seno, en otras palabras). Este hecho debe ayudarle a recordar cuál es cuál.
Tangente, cotangente, secante y cosecante requieren un poco más de esfuerzo que el seno y el coseno hacer. Para muchos ángulos en el círculo unitario, la evaluación de estas funciones requiere un trabajo cuidadoso con fracciones y raíces cuadradas. Recuerde siempre racionalizar el denominador para cualquier fracción en su respuesta final. Además, recuerde que cualquier número dividido por 0 no está definido. Las funciones tangentes y secantes, por ejemplo, no están definidos cuando el valor del coseno es 0. Del mismo modo, los valores cotangente y cosecante son indefinido cuando el valor del seno es 0.
Tiempo para un ejemplo. Para evaluar las seis funciones trigonométricas de 225 grados utilizando el círculo unidad, siga estos pasos:
Dibuja la imagen.
Cuando se le pide que encontrar la función trigonométrica de un ángulo, usted no tiene que dibujar un círculo unidad cada vez. En su lugar, utilice su inteligencia para descubrir la imagen. Para este ejemplo, 225 grados es de 45 grados más de 180 grados. Dibuja un triángulo 45-45-90 grados en apenas el tercer cuadrante.
Rellene las longitudes de las piernas y la hipotenusa.
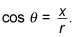Un triángulo 45er, ataviado como un árbol de Navidad.Utilice las reglas del triángulo 45er. La coordenada del punto en 225 grados es
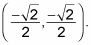
La figura muestra el triángulo, así como toda la información para evaluar las seis funciones trigonométricas.
¡Sé cuidadoso! Usa lo que sabes acerca de los ejes positivos y negativos en el plano de coordenadas para ayudarle. Debido a que el triángulo es en el tercer cuadrante, tanto el X y y Los valores deben ser negativos.
Encuentra el seno del ángulo.
El seno de un ángulo es la y valor, o la línea vertical que se extiende desde el punto en el círculo unitario a la X-eje. Para 225 grados, el y valor es
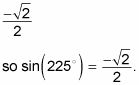
Encuentra el coseno del ángulo.
El valor del coseno es la X valor, por lo que debe ser
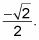
Encuentra la tangente del ángulo.
Para encontrar la tangente de un ángulo en la circunferencia unidad, se utiliza la definición alternativa de la tangente:
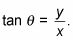
Otra forma de verlo es que
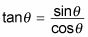
porque en el círculo unidad, la y valor es el seno y el X valor es el coseno. Así que si usted sabe el seno y el coseno de cualquier ángulo, también sabes la tangente. (Gracias, círculo unidad!) El seno y el coseno de 225 grados son a la vez
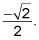
Por lo tanto, se puede dividir el seno por el coseno para obtener la tangente de 225 grados, que es 1.
Encuentra la cosecante del ángulo.
La cosecante de cualquier ángulo es
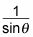
o r/y, mediante la definición de punto en el plano. Usando lo que determinó en el paso 1,
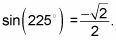
Ahora puede dividir 1 por
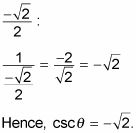
Encuentra la secante del ángulo.
El secante de cualquier ángulo es
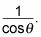
Debido a que el coseno de 225 grados es también
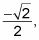
encontrado en el paso 4, la secante de 225 grados es
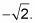
Encuentra la cotangente del ángulo.
La cotangente de un ángulo es
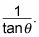
Desde el Paso 5, tan (225 grados) = 1. Así cuna (225 grados) = 1/1 = 1. Tan fácil como pastel!
-
La aplicación de las fórmulas de suma y diferencia de los cosenos para encontrar el coseno de la suma o diferencia de dos ángulos -
Cómo calcular un ángulo usando funciones trigonométricas recíprocas -
Cómo calcular el seno de ángulos especiales en grados -
¿Cómo encontrar la tangente de la suma o diferencia de ángulos -
Cómo graficar seno, coseno y tangente -
Cómo utilizar un ángulo de referencia para encontrar ángulos de soluciones
Cómo utilizar identidades medio ángulo para evaluar una función trigonométrica Puede utilizar identidades-medio ángulo para evaluar una función trigonométrica de un ángulo que no está en el círculo unitario utilizando uno que sea. Por ejemplo, 15 grados, que no es en el círculo unitario, es la mitad de 30 grados, que se…
Cómo utilizar SOHCAHTOA para encontrar las funciones trigonométricas de un triángulo rectángulo El estudio de la trigonometría comienza con el triángulo rectángulo. Las tres funciones principales trigonométricas (seno, coseno y tangente) y sus inversos (cosecante, secante y cotangente) todo lo que dicen algo acerca de las longitudes de los…
Asignar valores de la función trigonométrica negativos y positivos por cuadrante El primer paso para encontrar el valor de la función trigonométrica de uno de los ángulos que es un múltiplo de 30 o 45 grados es encontrar el ángulo de referencia en el círculo unitario. Cuando el ángulo de referencia viene a ser 0, 30, 45,…
Asignar funciones trigonométricas negativos y positivos por cuadrante Los valores de seno para 30, 150, 210 y 330 grados son 1/2, 1/2, -1/2 y -1/2, respectivamente. Todos estos múltiplos de 30 grados tienen un pecado cuyo valor absoluto del medio. La siguiente regla y figura ayudarle a determinar si un valor…
Tratar con identidades medio-ángulo que involucran radicales Mediante la adición, sustracción, o duplicando medidas de los ángulos, se puede encontrar gran cantidad de valores exactos de las funciones trigonométricas. Por ejemplo, puede utilizar la identidad de medio ángulo cuando el valor exacto de la…
Gama de funciones seno y coseno de dominio y Las funciones seno y coseno son únicos en el mundo de las funciones trigonométricas, porque sus relaciones siempre tienen un valor. No importa desde qué ángulo lo de entrada, se obtiene una salida resultante. El valor que se obtiene puede ser 0,…
Funciones trigonométricas secantes gama de Dominio y cosecante y Las funciones cosecante y secante están estrechamente ligados a seno y coseno, porque son los respectivos recíprocos. En referencia al plano de coordenadas, cosecante es r/y, y secante es r/X. El valor de r es la longitud de la hipotenusa de un…
Encuentra identidades trigonométricas opuesto ángulo los identidades de ángulo opuesto cambiar las funciones trigonométricas de ángulos negativos a las funciones de ángulos positivos. Ángulos negativos son grandes para describir una situación, pero no son realmente útil cuando se trata de pegar…
Cómo calcular las funciones trigonométricas de ángulos usando el círculo unitario Cálculo de funciones trigonométricas de ángulos dentro de un círculo unidad es muy fácil. La figura muestra un círculo unitario, que tiene la ecuación X2 + y2 = 1, junto con algunos puntos de la circunferencia y sus coordenadas.El uso de los…
Encontrar la función de la trigonometría de un ángulo en un círculo unitario Puede determinar las funciones trigonométricas de cualquier ángulo que se encuentran en el círculo unitario - cualquiera que se grafican en posición estándar (es decir, el vértice del ángulo está en el origen, y el lado inicial se encuentra…
Cómo utilizar identidades medio ángulo para encontrar el seno de un ángulo Mediante la adición, sustracción, o duplicando medidas de los ángulos, se puede encontrar gran cantidad de valores exactos de las funciones trigonométricas utilizando las funciones de ángulos que ya conoce. Por ejemplo, a pesar de que se puede…
Cómo utilizar la identidad de ángulo suma, cuando usted no sabe el ángulo En algunos problemas de trigonometría, usted no puede saber lo que la medida de un ángulo es, pero usted sabe algo acerca de valores de la función del ángulo. Por ejemplo, suponga que tiene dos ángulos, alfa en el segundo cuadrante de un…