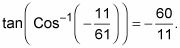¿Cómo resolver funciones trigonométricas inversas con ángulos poco comunes
Cuando se trabaja con funciones trigonométricas inversas, siempre es más conveniente cuando los números que está trabajando son los resultados de la aplicación de una de las funciones trigonométricas a una medida de ángulo común. Cuando el ángulo no es muy común, sin embargo, usted necesita una calculadora o una tabla.
Mediante el uso de las funciones trigonométricas inversas, puede resolver algunos problemas interesantes, en las que ni siquiera necesita saber la medida del ángulo. Usted sólo tiene que saber un valor de la función, un cuadrante, y algunas identidades trigonométricas. Por ejemplo, usted puede encontrar
que dice que
Usted no necesita saber la medida del ángulo de resolver este problema, pero sí es necesario saber el cuadrante que el lado del terminal se encuentra en, porque de lo contrario, dos ángulos diferentes pueden ser las respuestas correctas. El seno es positivo en los cuadrantes I y II, por lo que este problema podría consistir en un ángulo en cualquiera de esos cuadrantes, pero coseno no es positivo en esas dos cuadrantes. Considere el siguiente ejemplo.
Utilice la identidad de Pitágoras para encontrar el coseno del ángulo.
Ponga el valor por el pecado theta-, obtener el término coseno solo, y luego tomar la raíz cuadrada de ambos lados.
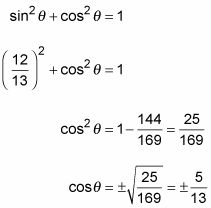
Elija el signo de la respuesta.
Debido lado terminal del ángulo está en QII y el coseno es negativo allí, la respuesta es
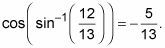
El cuadrante no es un misterio en un problema que utiliza la trigonometría inversa función. Encontrar
se puede suponer que el ángulo tiene su lado terminal en QII, ya que la función coseno inverso es negativo en ese cuadrante.
Utilice la identidad recíproca y recíproco del número para encontrar la secante.
El problema consiste en el ángulo cuyo coseno es
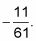
Llame al ángulo desconocido theta- y reescribir la expresión en términos del coseno theta- con esa medida. Escribe la expresión de esta manera con el fin de cambiar de una función trigonométrica inversa de una función trigonométrica para que pueda utilizar la identidad.
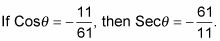
Utilice la identidad de Pitágoras para resolver la tangente.
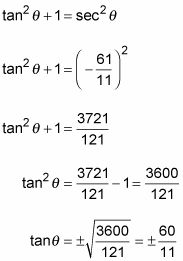
Elija el signo de la respuesta.
Debido a que el lado del terminal está en QII y la tangente es negativa en ese cuadrante,
-
Cómo calcular un ángulo utilizando funciones trigonométricas inversas -
¿Cómo encontrar funciones trigonométricas de un ángulo utilizando identidades pitagóricas -
Cómo utilizar un ángulo de referencia para encontrar ángulos de soluciones -
Cómo utilizar identidades medio ángulo para evaluar una función trigonométrica -
Cómo utilizar SOHCAHTOA para encontrar las funciones trigonométricas de un triángulo rectángulo -
Asignar valores de la función trigonométrica negativos y positivos por cuadrante
Asignar funciones trigonométricas negativos y positivos por cuadrante Los valores de seno para 30, 150, 210 y 330 grados son 1/2, 1/2, -1/2 y -1/2, respectivamente. Todos estos múltiplos de 30 grados tienen un pecado cuyo valor absoluto del medio. La siguiente regla y figura ayudarle a determinar si un valor…
Tratar con identidades medio-ángulo que involucran radicales Mediante la adición, sustracción, o duplicando medidas de los ángulos, se puede encontrar gran cantidad de valores exactos de las funciones trigonométricas. Por ejemplo, puede utilizar la identidad de medio ángulo cuando el valor exacto de la…
Gama de funciones seno y coseno de dominio y Las funciones seno y coseno son únicos en el mundo de las funciones trigonométricas, porque sus relaciones siempre tienen un valor. No importa desde qué ángulo lo de entrada, se obtiene una salida resultante. El valor que se obtiene puede ser 0,…
Sine Express en términos de coseno A pesar de que cada función de la trigonometría es perfectamente maravilloso, poder expresar cada función trig en términos de una de las otras cinco funciones trigonométricas es con frecuencia a su ventaja. Por ejemplo, usted puede tener…
Sine Express en términos de la tangente A pesar de que cada función de la trigonometría es perfectamente maravilloso, poder expresar cada función trig en términos de una de las otras cinco funciones trigonométricas es con frecuencia a su ventaja. Por ejemplo, usted puede tener…
Encuentra identidades trigonométricas opuesto ángulo los identidades de ángulo opuesto cambiar las funciones trigonométricas de ángulos negativos a las funciones de ángulos positivos. Ángulos negativos son grandes para describir una situación, pero no son realmente útil cuando se trata de pegar…
Ángulos gráfico en una posición estándar Navegantes, agrimensores, carpinteros y todos utilizan las mismas medidas de los ángulos, pero los ángulos comienzan en diferentes posiciones o lugares. En trigonometría y la mayoría de las otras disciplinas matemáticas, dibujar ángulos en una…
Funciones Gráfico de seno y coseno inversa Las gráficas de las funciones trigonométricas inversas son relativamente singularidad por ejemplo, seno inverso y el coseno inversa son un poco brusca y desarticulada. Estos gráficos son importantes debido a su impacto visual. Especialmente en el…
Cómo calcular los ángulos de referencia en grados Despejando el ángulo de referencia en grados es mucho más fácil que tratar de determinar una función trigonométrica del ángulo original. Para calcular la medida (en grados) del ángulo de referencia para cualquier ángulo theta dado, utilizar…
Cómo localizar ángulos de referencia Cada uno de los ángulos en un círculo unidad tiene un ángulo de referencia, que es siempre un ángulo agudo positivo (excepto los ángulos que ya son positivas y aguda). Al identificar el ángulo de referencia, se puede determinar los valores de…
Cómo utilizar la identidad de ángulo suma, cuando usted no sabe el ángulo En algunos problemas de trigonometría, usted no puede saber lo que la medida de un ángulo es, pero usted sabe algo acerca de valores de la función del ángulo. Por ejemplo, suponga que tiene dos ángulos, alfa en el segundo cuadrante de un…
Cómo utilizar las identidades de resta en un problema trig Usted puede encontrar valores de la función de los ángulos utilizando identidades ángulo de adición. Y usted tiene más posibilidades de encontrar los valores de la función de los ángulos cuando se utiliza la resta en un problema de…