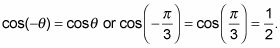Cómo utilizar las identidades de resta en un problema trig

Usted puede encontrar valores de la función de los ángulos utilizando identidades ángulo de adición. Y usted tiene más posibilidades de encontrar los valores de la función de los ángulos cuando se utiliza la resta en un problema de trigonometría. Por ejemplo, se puede determinar el seno de 15 grados mediante el uso de 45 grados y 30 grados y los valores de función y la identidad apropiada.

La resta o diferencia, las identidades encontrar la función de la diferencia entre los ángulos alfa y beta:

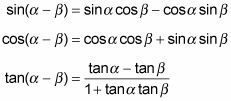
Observe cómo cada una de las identidades de resta se asemeja a su correspondiente identidad ángulo de suma. Por el teorema del seno, la señal entre los dos productos cambió de + a -, que parece tener sentido. Lo contrario es cierto para el coseno. La regla de adición para el coseno tiene - en ella, y la resta (o diferencia) regla tiene + en ella. La regla tangente tiene tanto + y - en la operación de IT en el numerador refleja el tipo de identidad.

Sólo las tres funciones trigonométricas originales tienen identidades diferencia realmente utilizables - la identidad de las funciones recíprocas son bastante darned complicado. Si desea que la diferencia de una función recíproca, la mejor opción es utilizar la identidad básica correspondiente y encontrar la inversa de la respuesta numérica después de que haya terminado todo.

Para ver una de las identidades de resta en acción, visita el siguiente ejemplo, que muestra cómo se puede encontrar el seno de 15 grados.

1. Determinar dos ángulos con una diferencia de 15 grados.

   Para simplificar las cosas, utilizar 45 y 30.

2. Sustituya los ángulos en la identidad para el seno de una diferencia.

   

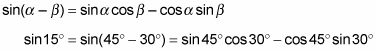
3. Reemplace los términos con los valores de la función y simplificar la respuesta.

   

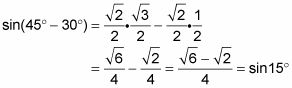
Usando radianes introduce fracciones a la imagen, como la búsqueda de bronceado pi-/ 12 mediante el uso de la identidad de la tangente de una diferencia.

1. Determine qué ángulos que necesita para obtener la diferencia.

   

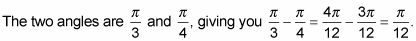
2. Sustituya los ángulos en la identidad de la tangente de la diferencia.

   

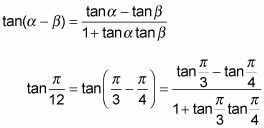
3. Reemplace los términos con los valores de la función y simplificar la respuesta.

   

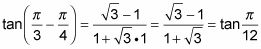
   El resultado es bastante desordenado. Se puede simplificar aún más multiplicando el numerador y el denominador por el conjugado (mismos términos, distinto signo) del denominador y simplificando el resultado:

   

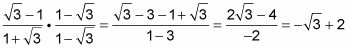
El siguiente ejemplo utiliza la identidad para el coseno de la diferencia junto con el ángulo de medición de 0 grados para determinar una identidad de ángulo opuesto. Esto demuestra la versatilidad y las identidades trigonométricas fáciles de usar son - y cómo todos ellos se llevan tan bien juntos.

En este ejemplo, encontrar

mediante el uso de la identidad de la diferencia entre los ángulos.

1. Determine qué ángulos que necesita para obtener la diferencia.

   Usando 0 y pi-/ 3 y restando con el 0 da primero un resultado negativo:

   

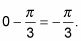
2. Sustituya los ángulos en la identidad para el coseno de la diferencia.

   

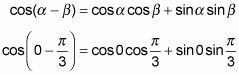
3. Vuelva a colocar los ángulos con los valores de la función y simplificar la respuesta.

   

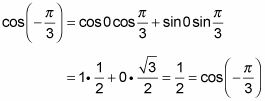
   Esta respuesta es exactamente lo que se obtiene si se utiliza la identidad de distinto ángulo de coseno: