¿Cómo simplificar una expresión utilizando par / impar identidades
Debido seno, coseno, y la tangente son funciones (funciones trigonométricas), que pueden definirse como pares o impares funciones. Sine y la tangente son funciones impares, y el coseno es una función par. En otras palabras,
pecado(-X) = -sen X
cos (-X) = Cos X
tan (-X) = -tan X
Estas identidades serán todos hacer apariciones en los problemas que le piden que simplificar una expresión, demostrar una identidad, o resolver una ecuación. ¿Cuál es la gran bandera roja? El hecho de que la variable dentro de la función trigonométrica es negativo. Cuando tan (-X), Por ejemplo, aparece en algún lugar de una expresión, por lo general se debe cambiar a -tan X.
Sobre todo, se utiliza incluso / impar identidades para fines de graficar, pero puede verlos en la simplificación de los problemas también. Se utiliza un par / impar identidad para simplificar cualquier expresión donde -X (o lo que sea la variable que se ve) está dentro de la función trigonométrica.
Los siguientes pasos muestran cómo simplificar [1 + sen (-X)] [1 - sen (-X)]:
Deshazte de todo el -X valores dentro de las funciones trigonométricas.
Se ven dos sin (-X) Funciones, por lo que los dos reemplazar con -sen X para obtener [1 + (-sen X)] [1 - (-sen X)].
Simplifique la nueva expresión.
Primero ajuste los dos signos negativos dentro de los paréntesis para obtener (1 - el pecado X) (1 + sin X) Y, a continuación, frustrar estos dos binomios para obtener 1 - pecado2 X.
Puedes buscar cualquier combinación de términos que podrían darle una identidad de Pitágoras.
Siempre que vea una función al cuadrado, usted debe pensar en las identidades pitagóricas. Las tres identidades pitagóricas son
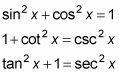
En cuanto a las identidades, se ve que 1 - pecado2 X es el mismo que cos2 X. Ahora la expresión está totalmente simplifica como cos2 X.
-
Incluso identidades y pico en las funciones trigonométricas -
Primeros pasos con identidades trigonométricas -
¿Cómo encontrar funciones trigonométricas de un ángulo utilizando identidades pitagóricas -
¿Cómo demostrar una igualdad mediante el uso de identidades periodicidad -
¿Cómo demostrar una igualdad usando identidades co-función -
¿Cómo demostrar una igualdad usando identidades pitagóricas
¿Cómo simplificar una expresión utilizando identidades de función co- Si usted toma la gráfica de y = Sen X y desplazar hacia la izquierda por pi / 2 unidades, se ve exactamente como la gráfica de y = Cos X. Lo mismo es cierto para la tangente y cotangente, así como secante y cosecante. Esa es la premisa básica de…
¿Cómo simplificar una expresión utilizando identidades recíprocas Cuando se le pregunta para simplificar una expresión que implica cosecante, secante o cotangente, cambia la expresión de funciones que implican seno, coseno, tangente o, respectivamente. Al cambiar las funciones de esta manera, usted está…
¿Cómo simplificar una expresión utilizando identidades periodicidad Identidades Periodicidad ilustrar cómo trasladar la gráfica de una función trigonométrica por un período a los resultados de izquierda o derecha en la misma función. Las funciones de seno, coseno, secante, cosecante y repetir cada 2 (pi)…
Cómo utilizar identidades para integrar las funciones trigonométricas Usted se sorprenderá de lo mucho que avanzar a menudo se puede hacer cuando se integra una función de trigonometría desconocida por primera ajustar usando las identidades Básica Cinco trig:El poder invisible de estas identidades se encuentra en…
Integrar, cuando los poderes de seno, coseno son aún, no negativo Cuando los poderes tanto de seno y coseno son uniformes y no negativo, se puede convertir el integrando en potencias impares de cosenos mediante el uso de las siguientes identidades trigonométricas.Dos identidades trigonométricas prácticos:Luego…
Identidades pitagóricas básicos para funciones trigonométricas Las identidades pitagóricas son bloques de construcción para muchas de las manipulaciones de ecuaciones y expresiones trigonométricas. Proporcionan un mayor número de métodos para resolver problemas trigonométricos de manera más eficiente, ya…
Sine Express en términos de secante o cosecante A pesar de que cada función trigonométrica es perfectamente maravilloso, poder expresar cada función trig en términos de una de las otras cinco funciones trigonométricas es con frecuencia a su ventaja. Por ejemplo, usted puede tener algunos…
Sine Express en términos de la tangente A pesar de que cada función de la trigonometría es perfectamente maravilloso, poder expresar cada función trig en términos de una de las otras cinco funciones trigonométricas es con frecuencia a su ventaja. Por ejemplo, usted puede tener…
Encuentra identidades relación trigonometría Trig tiene dos identidades llamados identidades de relación. Esta etiqueta puede ser confuso, ya que todas las funciones trigonométricas se definen por relaciones. En algún momento, sin embargo, los matemáticos pensaron que esta descripción era…
¿Cómo encontrar identidades medio-ángulo para tangente La media de ángulo trig identidad para tangente tiene dos versiones. En lugar de que esto sea una molestia, que tiene más de una opción es realmente bastante agradable, porque se puede elegir la versión que mejor se adapte a su situación. Las…
¿Cómo resolver una ecuación trigonométrica que tiene múltiples funciones trigonométricas Algunas ecuaciones de trigonometría contienen más de una función trigonométrica. Otros tienen mezclas de múltiples ángulos y ángulos individuales con la misma variable. Algunos ejemplos de tales ecuaciones incluyen 3cos2 X = Sen2 X, 2 seg X =…
Cómo utilizar las identidades de resta en un problema trig Usted puede encontrar valores de la función de los ángulos utilizando identidades ángulo de adición. Y usted tiene más posibilidades de encontrar los valores de la función de los ángulos cuando se utiliza la resta en un problema de…