¿Cómo simplificar una expresión utilizando identidades recíprocas
Cuando se le pregunta para simplificar una expresión que implica cosecante, secante o cotangente, cambia la expresión de funciones que implican seno, coseno, tangente o, respectivamente. Al cambiar las funciones de esta manera, usted está utilizando recíproca identidades. (Técnicamente, las identidades se trig funciones que acaba de pasar a ser considerado identidades, así, ya que ayudan a simplificar expresiones.) Utiliza las identidades recíprocas para que pueda cancelar las funciones y simplificar el problema.
La siguiente lista presenta estas identidades recíprocas:
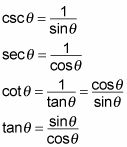
Cada relación de trig puede ser escrita como una combinación de los senos y / o cosenos, por lo que cambiar todas las funciones en una ecuación de senos y cosenos es la estrategia de simplificación que funciona con más frecuencia. Siempre trate de hacer este paso primero y luego mira a ver si las cosas se anulan y simplificar. Además, se trata de senos y cosenos suele ser más fácil si usted está buscando un denominador común para las fracciones. A partir de ahí, puede utilizar lo que sabe acerca de las fracciones para simplificar lo más que pueda.
Busque oportunidades para utilizar identidades recíprocas cuando el problema se te da contiene secante, cosecante o cotangente. Todas estas funciones se pueden escribir en términos de seno y coseno, y senos y cosenos son siempre el mejor lugar para empezar. Por ejemplo, puede utilizar identidades recíprocas para simplificar esta expresión:
Sigue estos pasos:
Cambie todas las funciones en las versiones de las funciones seno y coseno.
Debido a este problema implica una cosecante y cotangente, utiliza las identidades recíprocas para cambiar
Este proceso le da
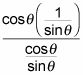
Romper la fracción compleja reescribiendo la barra de división que está presente en el problema original como
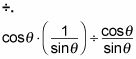
Invierta la última fracción y multiplicar.
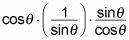
Cancelar las funciones para simplificar.
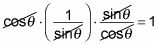
Los senos y cosenos se anulan, y se llega a 1 como su respuesta.
-
Incluso identidades y pico en las funciones trigonométricas -
Primeros pasos con identidades trigonométricas -
Cómo calcular un ángulo usando funciones trigonométricas recíprocas -
¿Cómo demostrar una igualdad mediante el uso de identidades periodicidad -
¿Cómo demostrar una igualdad usando identidades recíprocas -
¿Cómo demostrar una igualdad usando identidades co-función
¿Cómo demostrar identidades trigonométricas cuando se suman o restan términos Cuando se añaden o restan los términos en una prueba trig, puede crear fracciones donde no estaban antes. Esto es especialmente cierto cuando se trata de la secante y cosecante, porque se crea fracciones cuando se convierte (respectivamente)…
¿Cómo simplificar una expresión utilizando par / impar identidades Debido seno, coseno, y la tangente son funciones (funciones trigonométricas), que pueden definirse como pares o impares funciones. Sine y la tangente son funciones impares, y el coseno es una función par. En otras palabras,pecado(-X) = -sen Xcos…
¿Cómo simplificar una expresión utilizando identidades de función co- Si usted toma la gráfica de y = Sen X y desplazar hacia la izquierda por pi / 2 unidades, se ve exactamente como la gráfica de y = Cos X. Lo mismo es cierto para la tangente y cotangente, así como secante y cosecante. Esa es la premisa básica de…
¿Cómo simplificar una expresión utilizando identidades periodicidad Identidades Periodicidad ilustrar cómo trasladar la gráfica de una función trigonométrica por un período a los resultados de izquierda o derecha en la misma función. Las funciones de seno, coseno, secante, cosecante y repetir cada 2 (pi)…
Cómo simplificar expresiones trigonométricas con un binomio en el denominador de una fracción Cuando una expresión trigonométrica es una fracción con un binomio en su denominador, siempre tenga en cuenta multiplicando por el conjugado antes de hacer cualquier otra cosa. La mayoría de las veces, esta técnica permite simplificar.Por…
Cómo utilizar identidades para integrar las funciones trigonométricas Usted se sorprenderá de lo mucho que avanzar a menudo se puede hacer cuando se integra una función de trigonometría desconocida por primera ajustar usando las identidades Básica Cinco trig:El poder invisible de estas identidades se encuentra en…
Cambie de senos y cosenos en una identidad trigonometría Con algunas identidades trigonométricas, usted puede decidir para simplificar las cosas, ya sea cambiando todo para senos y cosenos o factoring a cabo alguna función. A veces, no está claro de qué lado usted debe trabajar en o lo que debe hacer…
Cotangente y cosecante identidades en un círculo unitario A partir de la identidad de Pitágoras, el pecado2theta- + cos2theta- = 1, puede derivar cotangente y cosecante identidades pitagóricas. Todo lo que hacemos es tirar un poco de álgebra y aplicar las identidades recíprocas y de relación y -…
Sine Express en términos de secante o cosecante A pesar de que cada función trigonométrica es perfectamente maravilloso, poder expresar cada función trig en términos de una de las otras cinco funciones trigonométricas es con frecuencia a su ventaja. Por ejemplo, usted puede tener algunos…
Encuentra identidades relación trigonometría Trig tiene dos identidades llamados identidades de relación. Esta etiqueta puede ser confuso, ya que todas las funciones trigonométricas se definen por relaciones. En algún momento, sin embargo, los matemáticos pensaron que esta descripción era…
¿Cómo encontrar identidades medio-ángulo para tangente La media de ángulo trig identidad para tangente tiene dos versiones. En lugar de que esto sea una molestia, que tiene más de una opción es realmente bastante agradable, porque se puede elegir la versión que mejor se adapte a su situación. Las…
Cómo utilizar las identidades de resta en un problema trig Usted puede encontrar valores de la función de los ángulos utilizando identidades ángulo de adición. Y usted tiene más posibilidades de encontrar los valores de la función de los ángulos cuando se utiliza la resta en un problema de…