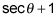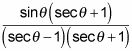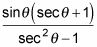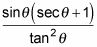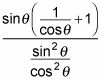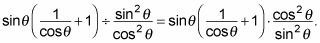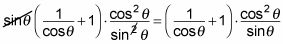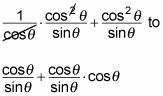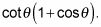Cómo simplificar expresiones trigonométricas con un binomio en el denominador de una fracción
Cuando una expresión trigonométrica es una fracción con un binomio en su denominador, siempre tenga en cuenta multiplicando por el conjugado antes de hacer cualquier otra cosa. La mayoría de las veces, esta técnica permite simplificar.
Por ejemplo, siga los pasos para volver a escribir esta expresión sin una fracción:
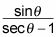
Multiplica el numerador y el denominador por el conjugado del denominador.
El conjugado de la + b es la - b, y viceversa. Así que hay que multiplicar por
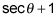
en la parte superior e inferior de la fracción. Este paso le da
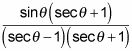
Foil los conjugados.
Recuerde que cuando usted papel de aluminio, se multiplica el primero, afuera, adentro, y último términos juntos.
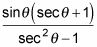
Cambie las identidades de sus formas más simples.
El uso de la identidad en la parte inferior, se obtiene
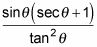
Cambie todas las funciones trig para senos y cosenos.
Aquí se vuelve más complejo:
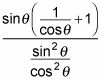
Cambie la gran barra de división a un signo de división, y luego invertir la fracción para que pueda multiplicar su lugar.
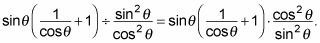
Cancelar lo que pueda de la expresión.
El seno en la parte superior anula uno de los senos en la parte inferior, la deja con la siguiente ecuación:
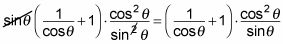
Distribuir y ver qué pasa!
A través de las cancelaciones, se pasa de
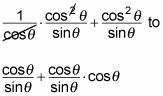
Esta expresión finalmente se simplifica a

Y si se le pide que tomarlo incluso un paso más allá, puede factorizar llegar
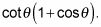
Sobre el autor
 ¿Cómo demostrar una igualdad usando identidades co-función
¿Cómo demostrar una igualdad usando identidades co-función Identidades Co-función pueden aparecer en trig pruebas. Si usted ve la expresión pi / 2 - X paréntesis dentro de cualquier función trigonométrica, es necesario utilizar una identidad co-función para la prueba. Siga los pasos para demostrar…
 ¿Cómo demostrar identidades trigonométricas cuando usted comienza con fracciones
¿Cómo demostrar identidades trigonométricas cuando usted comienza con fracciones Cuando la expresión trig te dan comienza con fracciones, la mayoría de las veces usted tiene que agregar (o restar) a conseguir cosas para simplificar. He aquí un ejemplo de una prueba donde hacer precisamente eso recupera el balón rodando.…
 Cómo racionalizar un radical de un denominador
Cómo racionalizar un radical de un denominador Una convención de las matemáticas es que usted no deja radicales en el denominador de una expresión cuando se escribe en su forma final. Así que hacemos algo que se llama racionalizar el denominador. Esta convención hace que la recogida como…
 ¿Cómo simplificar una expresión utilizando identidades recíprocas
¿Cómo simplificar una expresión utilizando identidades recíprocas Cuando se le pregunta para simplificar una expresión que implica cosecante, secante o cotangente, cambia la expresión de funciones que implican seno, coseno, tangente o, respectivamente. Al cambiar las funciones de esta manera, usted está…
 ¿Cómo resolver los límites de la multiplicación conjugada
¿Cómo resolver los límites de la multiplicación conjugada Para resolver ciertos problemas de límite, tendrá la técnica de multiplicación conjugado. Cuando la sustitución no funciona en la función original - por lo general a causa de un agujero en la función - se puede usar la multiplicación…
 Cómo utilizar identidades para integrar las funciones trigonométricas
Cómo utilizar identidades para integrar las funciones trigonométricas Usted se sorprenderá de lo mucho que avanzar a menudo se puede hacer cuando se integra una función de trigonometría desconocida por primera ajustar usando las identidades Básica Cinco trig:El poder invisible de estas identidades se encuentra en…
 Cambie de senos y cosenos en una identidad trigonometría
Cambie de senos y cosenos en una identidad trigonometría Con algunas identidades trigonométricas, usted puede decidir para simplificar las cosas, ya sea cambiando todo para senos y cosenos o factoring a cabo alguna función. A veces, no está claro de qué lado usted debe trabajar en o lo que debe hacer…
 Sine Express en términos de secante o cosecante
Sine Express en términos de secante o cosecante A pesar de que cada función trigonométrica es perfectamente maravilloso, poder expresar cada función trig en términos de una de las otras cinco funciones trigonométricas es con frecuencia a su ventaja. Por ejemplo, usted puede tener algunos…
 Sine Express en términos de cotangente
Sine Express en términos de cotangente A pesar de que cada función de la trigonometría es perfectamente maravilloso, poder expresar cada función trig en términos de una de las otras cinco funciones trigonométricas es con frecuencia a su ventaja. Por ejemplo, usted puede tener…
 ¿Cómo encontrar un común denominador de una fracción de resolver una identidad trigonométrica
¿Cómo encontrar un común denominador de una fracción de resolver una identidad trigonométrica Las fracciones son tus amigos. Usted no puede creer esto, pero cuanto más se trabaja con funciones de trigonometría, más te gusta fracciones. Encontrar un denominador común combinar fracciones menudo allana el camino a la solución de una…
 ¿Cómo encontrar identidades medio-ángulo para tangente
¿Cómo encontrar identidades medio-ángulo para tangente La media de ángulo trig identidad para tangente tiene dos versiones. En lugar de que esto sea una molestia, que tiene más de una opción es realmente bastante agradable, porque se puede elegir la versión que mejor se adapte a su situación. Las…
 Cómo multiplicar por un conjugado de encontrar una identidad trigonometría
Cómo multiplicar por un conjugado de encontrar una identidad trigonometría Conjugados ofrecen una gran manera de encontrar identidades trigonométricas. En matemáticas, un conjugado formado por los mismos dos términos como la primera expresión, separados por el signo opuesto. Por ejemplo, el conjugado deEn trig,…