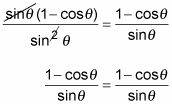Cómo multiplicar por un conjugado de encontrar una identidad trigonometría
Conjugados ofrecen una gran manera de encontrar identidades trigonométricas. En matemáticas, un conjugado formado por los mismos dos términos como la primera expresión, separados por el signo opuesto. Por ejemplo, el conjugado de
En trig, multiplicando el numerador y el denominador de una fracción por un conjugado puede crear algunos resultados realmente agradables.
Por ejemplo, multiplicando por un conjugado es una forma rápida, fácil de resolver la identidad
Multiplicar el numerador y el denominador de la fracción de la izquierda por el conjugado del denominador.
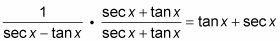
Los dos denominadores multiplicados juntos son la diferencia de dos cuadrados.
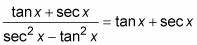
Reemplace seg2 X en el denominador con su equivalente mediante el uso de la identidad de Pitágoras.
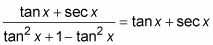
Simplifique el denominador mediante la cancelación de los dos opuestos.
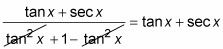
En el siguiente ejemplo, usted tiene que decidir qué fracción multiplicar el conjugado por. En este ejemplo se elige la fracción a la derecha, debido a que el conjugado del numerador de la derecha es visible en el denominador de la izquierda. Resolver la identidad
Multiplica el numerador y el denominador de la fracción a la derecha por el conjugado del numerador.
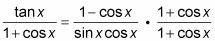
Multiplique las fracciones juntos, manteniendo los paréntesis en el denominador.
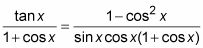
Sustituya el equivalente de la identidad de Pitágoras en el numerador de la fracción a la derecha. Luego reducir la fracción.
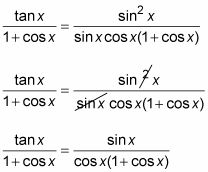
Vuelva a escribir la fracción a la derecha como un producto de dos fracciones, arreglando cuidadosamente los factores.
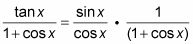
Vuelva a colocar la primera fracción a la derecha con su equivalente relación de identidad. Vuelva a escribir la expresión como una fracción.
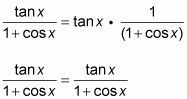
La identidad de ángulo medio para la función tangente tiene dos formas diferentes. Multiplicando por el conjugado es un buen método para mostrar que estas dos formas son equivalentes. El siguiente ejemplo demuestra que
Multiplicar el numerador y el denominador de la fracción de la izquierda por el conjugado del denominador.
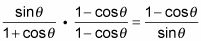
Multiplique los dos denominadores juntos, pero deje el numerador en forma factorizada.
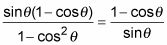
Reemplace el denominador de la izquierda con su equivalente mediante el uso de la identidad de Pitágoras.
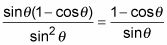
Reducir la fracción de la izquierda.
Cómo restar fracciones con el mismo denominador Restar fracciones con el mismo denominador (número inferior) es fácil. Cuando los denominadores son los mismos, sólo puede pensar en las fracciones como pedazos de torta.Para restar una fracción de otro cuando ambos tienen el mismo denominador,…
¿Cómo distinguir expresiones racionales propias e impropias Integración por fracciones parciales sólo funciona con expresiones racionales adecuadas, pero no con expresiones racionales impropias. Decirle a una fracción propia a partir de uno inadecuada es fácil: Una fracción a / b es correcta si el…
Cómo racionalizar un radical de un denominador Una convención de las matemáticas es que usted no deja radicales en el denominador de una expresión cuando se escribe en su forma final. Así que hacemos algo que se llama racionalizar el denominador. Esta convención hace que la recogida como…
Cómo simplificar expresiones trigonométricas con un binomio en el denominador de una fracción Cuando una expresión trigonométrica es una fracción con un binomio en su denominador, siempre tenga en cuenta multiplicando por el conjugado antes de hacer cualquier otra cosa. La mayoría de las veces, esta técnica permite simplificar.Por…
¿Cómo resolver los límites de la multiplicación conjugada Para resolver ciertos problemas de límite, tendrá la técnica de multiplicación conjugado. Cuando la sustitución no funciona en la función original - por lo general a causa de un agujero en la función - se puede usar la multiplicación…
Romper o combinar fracciones para resolver una identidad trigonometría Una identidad trigonométrica con fracciones puede trabajar a su ventaja- te dan una plan de ataque. Usted puede trabajar hacia la eliminación de la fracción y, en el proceso, resolver el problema. Dos de las principales técnicas para trabajar…
Cambie de senos y cosenos en una identidad trigonometría Con algunas identidades trigonométricas, usted puede decidir para simplificar las cosas, ya sea cambiando todo para senos y cosenos o factoring a cabo alguna función. A veces, no está claro de qué lado usted debe trabajar en o lo que debe hacer…
¿Cómo encontrar un común denominador de una fracción de resolver una identidad trigonométrica Las fracciones son tus amigos. Usted no puede creer esto, pero cuanto más se trabaja con funciones de trigonometría, más te gusta fracciones. Encontrar un denominador común combinar fracciones menudo allana el camino a la solución de una…
¿Cómo encontrar identidades medio-ángulo para tangente La media de ángulo trig identidad para tangente tiene dos versiones. En lugar de que esto sea una molestia, que tiene más de una opción es realmente bastante agradable, porque se puede elegir la versión que mejor se adapte a su situación. Las…
Cómo cuadrar ambas partes para resolver un problema de identidad trigonometría Cuando se trabaja en ambos lados de una identidad trigonométrica, al mismo tiempo, es posible que a veces tenga que cuadrar ambos lados. Por lo general, utilizar esta técnica cuando un lado o el otro (o ambos) tiene un radical. Este método…
¿Cómo trabajar ambos lados de una identidad trig Con una identidad trigonometría, trabajando en ambos lados de la ecuación es aún más divertido que trabajar en ambos lados de una algebraico ecuación. En álgebra, puede multiplicar cada lado por el mismo número, cuadrado ambos lados, añadir…
Preparación ASVAB: cómo sumar y restar fracciones Adición y sustracción de fracciones para el ASVAB (o para cualquier otro propósito) puede ser tan simple como multiplicar y dividir, o puede ser más difícil. A medida que la siguiente información muestra, todo depende de si las fracciones…