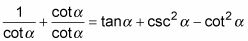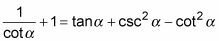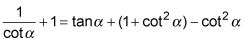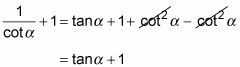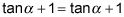¿Cómo trabajar ambos lados de una identidad trig
Con una identidad trigonometría, trabajando en ambos lados de la ecuación es aún más divertido que trabajar en ambos lados de una algebraico ecuación. En álgebra, puede multiplicar cada lado por el mismo número, cuadrado ambos lados, añadir o restar lo mismo a cada lado, y así sucesivamente. Cuando resolvemos Trig identidades y ecuaciones, puede usar todas esas reglas de álgebra más usted puede hacer sustituciones con las diversas identidades trigonométricas cuando los necesite. Incluso puede insertar una identidad diferente en cada lado - el gran ventaja de trabajar en ambos lados de una identidad trig.
Este primer ejemplo es bastante básico, pero tiene la idea de diámetro. Resolver la identidad
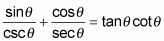
trabajando ambos lados.
Cambie las funciones que no son una de las tres funciones básicas mediante el uso de sus identidades recíprocas.
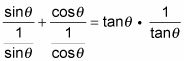
Simplifique las dos fracciones de la izquierda por voltear los denominadores y multiplicándolos por sus numeradores.
Luego multiplique los dos factores de la derecha juntos.
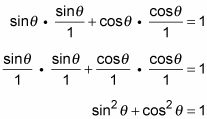
Vuelva a colocar la suma de la izquierda mediante el uso de la identidad de Pitágoras.
Se termina con 1 = 1.
En el siguiente ejemplo, se cambia todo para senos y cosenos. Demostrar la identidad
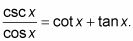
Cambie las funciones a sus equivalencias mediante el uso de las identidades recíprocas y de relación.
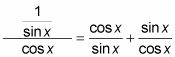
A la izquierda, girar el denominador y se multiplica por el numerador.
A la derecha, multiplicar cada fracción por una fracción igual a 1 (utilizando el denominador de la otra fracción) para obtener denominadores comunes para todas las fracciones.
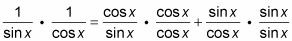
Simplificar las fracciones multiplicadas.
Añadir las dos fracciones de la derecha juntos.
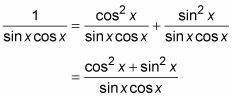
Reemplace el numerador a la derecha con el valor de la identidad de Pitágoras.
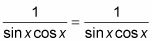
Este último ejemplo requiere un poco de creatividad para hacer el trabajo. Pero trabajar en ambos lados todavía funciona mejor cuando se demuestra que la siguiente es una identidad:
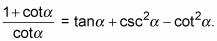
Dividir la fracción de la izquierda escribiendo cada término en el numerador sobre el denominador.
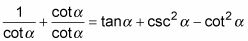
Reducir la segunda fracción a 1.
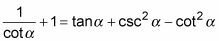
Vuelva a colocar el csc2 a la derecha con su equivalente mediante el uso de la identidad de Pitágoras.
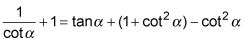
Simplificar los términos de la derecha - dos son opuestos el uno del otro.
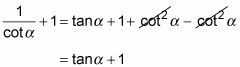
Reemplace la fracción de la izquierda mediante el uso de la identidad recíproca.
-
Consejos de matemáticas básicas: fracciones -
¿Cómo aumentar los términos de una fracción -
Primeros pasos con identidades trigonométricas -
¿Cómo demostrar una igualdad mediante el uso de identidades periodicidad -
¿Cómo demostrar una igualdad usando identidades co-función -
¿Cómo demostrar identidades complejas, trabajando los distintos lados de una prueba trig
¿Cómo demostrar una igualdad usando identidades pitagóricas Cuando se le preguntó para demostrar una identidad, si usted ve un negativo de una variable dentro de una función trigonométrica, se utiliza automáticamente un par / impar identidad. En primer lugar, sustituir todas las funciones…
¿Cómo demostrar identidades trigonométricas cuando usted comienza con fracciones Cuando la expresión trig te dan comienza con fracciones, la mayoría de las veces usted tiene que agregar (o restar) a conseguir cosas para simplificar. He aquí un ejemplo de una prueba donde hacer precisamente eso recupera el balón rodando.…
¿Cómo simplificar una expresión utilizando identidades periodicidad Identidades Periodicidad ilustrar cómo trasladar la gráfica de una función trigonométrica por un período a los resultados de izquierda o derecha en la misma función. Las funciones de seno, coseno, secante, cosecante y repetir cada 2 (pi)…
Romper o combinar fracciones para resolver una identidad trigonometría Una identidad trigonométrica con fracciones puede trabajar a su ventaja- te dan una plan de ataque. Usted puede trabajar hacia la eliminación de la fracción y, en el proceso, resolver el problema. Dos de las principales técnicas para trabajar…
Cambie de senos y cosenos en una identidad trigonometría Con algunas identidades trigonométricas, usted puede decidir para simplificar las cosas, ya sea cambiando todo para senos y cosenos o factoring a cabo alguna función. A veces, no está claro de qué lado usted debe trabajar en o lo que debe hacer…
Sine Express en términos de cotangente A pesar de que cada función de la trigonometría es perfectamente maravilloso, poder expresar cada función trig en términos de una de las otras cinco funciones trigonométricas es con frecuencia a su ventaja. Por ejemplo, usted puede tener…
¿Cómo encontrar un común denominador de una fracción de resolver una identidad trigonométrica Las fracciones son tus amigos. Usted no puede creer esto, pero cuanto más se trabaja con funciones de trigonometría, más te gusta fracciones. Encontrar un denominador común combinar fracciones menudo allana el camino a la solución de una…
¿Cómo encontrar identidades medio-ángulo para tangente La media de ángulo trig identidad para tangente tiene dos versiones. En lugar de que esto sea una molestia, que tiene más de una opción es realmente bastante agradable, porque se puede elegir la versión que mejor se adapte a su situación. Las…
Cómo multiplicar por un conjugado de encontrar una identidad trigonometría Conjugados ofrecen una gran manera de encontrar identidades trigonométricas. En matemáticas, un conjugado formado por los mismos dos términos como la primera expresión, separados por el signo opuesto. Por ejemplo, el conjugado deEn trig,…
Cómo eliminar un tercer ángulo para resolver una identidad trigonometría Identidades de suma y diferencia por lo general implican dos ángulos diferentes y luego un tercer ángulo combinado. Al probar estas identidades trigonométricas, a menudo es necesario deshacerse de ese tercer ángulo. El siguiente ejemplo trata de…
¿Cómo resolver una ecuación trigonométrica que tiene múltiples funciones trigonométricas Algunas ecuaciones de trigonometría contienen más de una función trigonométrica. Otros tienen mezclas de múltiples ángulos y ángulos individuales con la misma variable. Algunos ejemplos de tales ecuaciones incluyen 3cos2 X = Sen2 X, 2 seg X =…
Cómo cuadrar ambos lados de una ecuación trigonométrica Cuando la resolución de ecuaciones de trigonometría, más de un método generalmente funciona - a pesar de un método es a menudo más rápido o más fácil que otro. Con la práctica, usted obtendrá buenos en la elección de la mejor de las…
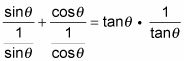
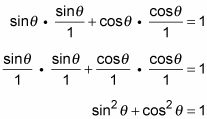
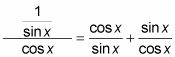
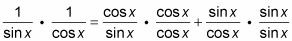
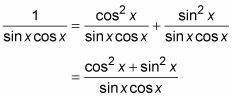
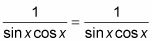