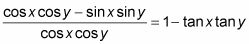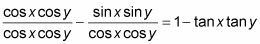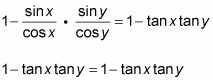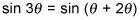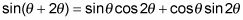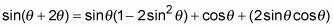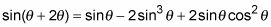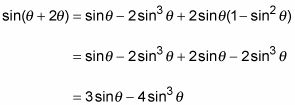Cómo eliminar un tercer ángulo para resolver una identidad trigonometría
Identidades de suma y diferencia por lo general implican dos ángulos diferentes y luego un tercer ángulo combinado. Al probar estas identidades trigonométricas, a menudo es necesario deshacerse de ese tercer ángulo. El siguiente ejemplo trata de una suma de dos ángulos diferentes.
Reemplazar el coseno de la suma de los dos ángulos con su identidad.
Romper la fracción poniendo cada término en el numerador sobre el denominador.
Reduzca la primera fracción. Vuelva a escribir la segunda fracción como el producto de dos fracciones. A continuación, reemplace las dos fracciones en que el producto mediante el uso de la identidad relación.
El siguiente ejemplo muestra una identidad por tres veces un ángulo: sin3theta- = 3sintheta- - 4 pecado3theta-.
Vuelva a colocar la 3theta- con la suma de theta- y 2theta- para crear la identidad de la suma de dos ángulos.
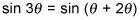
Aplicar la identidad ángulo de suma para el seno.
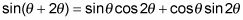
Ahora reemplace cos2theta- y sin2theta- utilizando las identidades de doble ángulo.
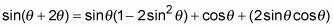
Tienes que elegir la identidad adecuada para el cos2theta-. En este ejemplo, desea que el resultado final sea todos los senos de el mismo ángulo.
Multiplicar un pase desde la banda derecha.
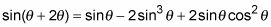
Reemplace cos2theta- con su equivalente mediante el uso de la identidad de Pitágoras. Entonces simplificar los términos.
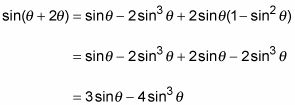
Sobre el autor
 Cambie de senos y cosenos en una identidad trigonometría
Cambie de senos y cosenos en una identidad trigonometría Con algunas identidades trigonométricas, usted puede decidir para simplificar las cosas, ya sea cambiando todo para senos y cosenos o factoring a cabo alguna función. A veces, no está claro de qué lado usted debe trabajar en o lo que debe hacer…
 Tratar con identidades medio-ángulo que involucran radicales
Tratar con identidades medio-ángulo que involucran radicales Mediante la adición, sustracción, o duplicando medidas de los ángulos, se puede encontrar gran cantidad de valores exactos de las funciones trigonométricas. Por ejemplo, puede utilizar la identidad de medio ángulo cuando el valor exacto de la…
 Encuentra identidades trigonométricas opuesto ángulo
Encuentra identidades trigonométricas opuesto ángulo los identidades de ángulo opuesto cambiar las funciones trigonométricas de ángulos negativos a las funciones de ángulos positivos. Ángulos negativos son grandes para describir una situación, pero no son realmente útil cuando se trata de pegar…
 ¿Cómo encontrar un común denominador de una fracción de resolver una identidad trigonométrica
¿Cómo encontrar un común denominador de una fracción de resolver una identidad trigonométrica Las fracciones son tus amigos. Usted no puede creer esto, pero cuanto más se trabaja con funciones de trigonometría, más te gusta fracciones. Encontrar un denominador común combinar fracciones menudo allana el camino a la solución de una…
 ¿Cómo encontrar identidades medio-ángulo para tangente
¿Cómo encontrar identidades medio-ángulo para tangente La media de ángulo trig identidad para tangente tiene dos versiones. En lugar de que esto sea una molestia, que tiene más de una opción es realmente bastante agradable, porque se puede elegir la versión que mejor se adapte a su situación. Las…
 Cómo multiplicar por un conjugado de encontrar una identidad trigonometría
Cómo multiplicar por un conjugado de encontrar una identidad trigonometría Conjugados ofrecen una gran manera de encontrar identidades trigonométricas. En matemáticas, un conjugado formado por los mismos dos términos como la primera expresión, separados por el signo opuesto. Por ejemplo, el conjugado deEn trig,…
 ¿Cómo resolver una ecuación trigonométrica que tiene múltiples funciones trigonométricas
¿Cómo resolver una ecuación trigonométrica que tiene múltiples funciones trigonométricas Algunas ecuaciones de trigonometría contienen más de una función trigonométrica. Otros tienen mezclas de múltiples ángulos y ángulos individuales con la misma variable. Algunos ejemplos de tales ecuaciones incluyen 3cos2 X = Sen2 X, 2 seg X =…
 Cómo utilizar identidades medio ángulo para encontrar el seno de un ángulo
Cómo utilizar identidades medio ángulo para encontrar el seno de un ángulo Mediante la adición, sustracción, o duplicando medidas de los ángulos, se puede encontrar gran cantidad de valores exactos de las funciones trigonométricas utilizando las funciones de ángulos que ya conoce. Por ejemplo, a pesar de que se puede…
 Cómo utilizar la identidad de ángulo suma, cuando usted no sabe el ángulo
Cómo utilizar la identidad de ángulo suma, cuando usted no sabe el ángulo En algunos problemas de trigonometría, usted no puede saber lo que la medida de un ángulo es, pero usted sabe algo acerca de valores de la función del ángulo. Por ejemplo, suponga que tiene dos ángulos, alfa en el segundo cuadrante de un…
 Cómo utilizar la identidad de doble ángulo para el seno
Cómo utilizar la identidad de doble ángulo para el seno La fórmula de doble ángulo para el seno proviene del uso de la identidad trigonométrica para el seno de una suma, el pecado (alfa + beta-) = sinalpha-cosbeta- +-cosalpha sinbeta-. Si alfa = beta-, entonces se puede sustituir beta- con alfa en la…
 Cómo utilizar las identidades de resta en un problema trig
Cómo utilizar las identidades de resta en un problema trig Usted puede encontrar valores de la función de los ángulos utilizando identidades ángulo de adición. Y usted tiene más posibilidades de encontrar los valores de la función de los ángulos cuando se utiliza la resta en un problema de…
 ¿Cómo trabajar ambos lados de una identidad trig
¿Cómo trabajar ambos lados de una identidad trig Con una identidad trigonometría, trabajando en ambos lados de la ecuación es aún más divertido que trabajar en ambos lados de una algebraico ecuación. En álgebra, puede multiplicar cada lado por el mismo número, cuadrado ambos lados, añadir…
![]()