Primeros pasos con identidades trigonométricas

Es necesario familiarizarse con las posibilidades de volver a escribir expresiones trigonométricas. Un trig identidad es realmente una expresión equivalente o la forma de una función que se puede utilizar en lugar del original. El formato equivalente puede hacer más fácil el factoring, la resolución de una solicitud que sea posible, y (más tarde) la realización de una operación en el cálculo más manejable.

Las identidades trigonométricas se dividen en muchas clasificaciones diferentes. Estos grupos ayudan a recordar las identidades y hacer la determinación de que la identidad de usar en un cambio concreto más fácil.

En un problema de identidad trigonométrica clásico, intenta hacer que un lado de la ecuación coincide con el otro lado. La mejor manera de hacerlo es trabajar en un solo lado - la izquierda oa la derecha - pero a veces tienes que trabajar en ambos lados para ver exactamente cómo funciona el problema hasta el final.

En pre-cálculo, que vamos a trabajar con las identidades trigonométricas básicas de las siguientes maneras:

• Determinar qué funciones trigonométricas son recíprocos el uno del otro

• La creación de identidades pitagóricas de un triángulo rectángulo cuya hipotenusa mide 1 unidad

• La determinación de la señal de identidades cuya medida del ángulo es negado

• Coincidencia hasta trig funciones y sus compañeros de funciones

• El uso de los períodos de funciones en las identidades

• Aprovechar al máximo de sustituciones seleccionadas en identidades

• Trabajando en un solo lado de la identidad

• Averiguar dónde ir con una identidad, trabajando ambos lados a la vez

No deje que los errores comunes viaje que UP- tener en cuenta que cuando se trabaja en las identidades trigonométricas, algunos desafíos incluirán lo siguiente:

• Hacer un seguimiento de donde el 1 va en las identidades pitagóricas

• Recordando el término medio cuando la cuadratura binomios que involucran funciones trigonométricas

• Reescribir correctamente identidades pitagóricas en la resolución de un término al cuadrado

• Reconociendo la notación exponente

Problemas de práctica

1. Demostrar la identidad trigonométrica. Indique su primera sustitución de identidad:

   

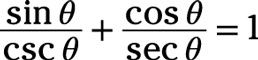
   Responder: utilizar la identidad recíproca

   Debido a que cada término contiene una función y su recíproco, utilizando identidades recíprocas simplificará los términos rápidamente.

   En primer lugar, sustituir

   

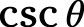
   con su identidad recíproca,

   

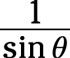
   y

   

   con su identidad recíproca:

   

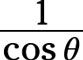
   Entonces simplificar las fracciones complejas.

   

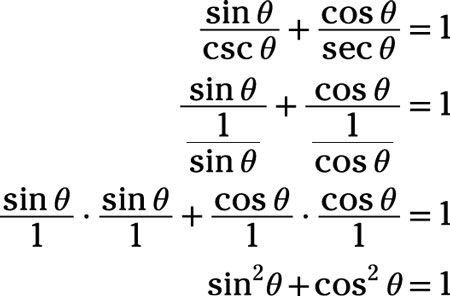
   Por último, vuelva a colocar

   

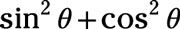
   con 1, utilizando la identidad de Pitágoras: 1 = 1

2. Determinar el término faltante o factor de la identidad, cambiando todas las funciones a las que utilizan seno o coseno:

   

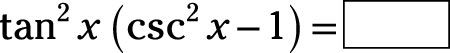
   Responder: 1

   Utilice la identidad recíproca para reemplazar csc²X y utilizar la identidad relación para reemplazar bronceado²X:

   

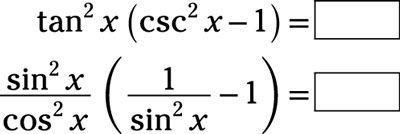
   Distribuir

   

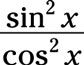
   simplificar y luego combinar los dos términos:

   

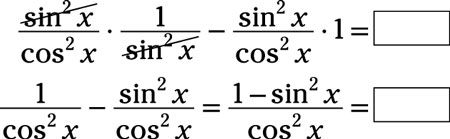
   Vuelva a escribir la identidad de Pitágoras, el pecado²X + cos²X = 1, el pecado restando²X de cada lado para llegar cos²X = 1 - sen²X. Reemplace el numerador de la fracción en la identidad con cos²X:

   

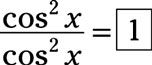
   El término que falta es 1.