¿Cómo resolver una ecuación trigonométrica que tiene múltiples funciones trigonométricas

Algunas ecuaciones de trigonometría contienen más de una función trigonométrica. Otros tienen mezclas de múltiples ángulos y ángulos individuales con la misma variable. Algunos ejemplos de tales ecuaciones incluyen 3cos² X = Sen² X, 2 seg X = Tan X + cuna X, cos 2X + cos X + 1 = 0, y el pecado X cos X = 1/2.

Para obtener estas ecuaciones en formas más manejables para que pueda utilizar el factoring u otro método para resolverlos, se utiliza identidades para sustituir parte o la totalidad de los términos. Por ejemplo, para resolver 3cos² X = Sen² X para todos los ángulos entre 0 y 2pi-, aplicar una identidad de Pitágoras.

1. Reemplace el término pecado² X con su equivalente de la identidad de Pitágoras, el pecado² X + cos² X = 1 o el pecado² X = 1 - cos² X.

   3cos² X = 1 - cos² X

2. Añadir cos² X a cada lado y simplificar dividiendo.

   

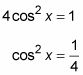
3. Toma la raíz cuadrada de cada lado.

   

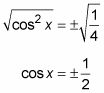
4. Resuelva para los valores de X que satisfacen la ecuación.

   

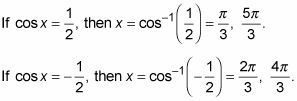
En el siguiente ejemplo, se empieza con tres funciones trigonométricas diferentes. Una buena táctica es reemplazar cada función utilizando ya sea una identidad ratio o una identidad recíproca. El uso de estas identidades crea fracciones y fracciones requieren denominadores comunes.

Por cierto, que tienen fracciones de ecuaciones trigonométricas es bien, porque los productos que resultan de multiplicar y hacer fracciones equivalentes son generalmente partes de identidades que a continuación, puede sustituir en para hacer la expresión más simple. Resuelva 2 seg X = Tan X + cuna X para todas las posibles soluciones en grados.

1. Vuelva a colocar cada término con su respectiva identidad recíproca o la relación.

   

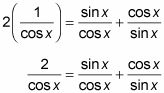
2. Vuelva a escribir las fracciones con el pecado común denominador X cos X.

   Multiplica cada término por una fracción que es igual a 1, con cualquiera de seno o coseno tanto en el numerador y el denominador.

   

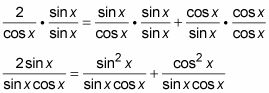
3. Añadir las dos fracciones de la derecha. Luego, utilizando la identidad de Pitágoras, reemplace el nuevo numerador con 1.

   

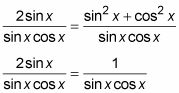
4. Establezca la ecuación igual a 0 restando el término correcto de cada lado.

   

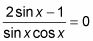
5. Ahora configure el numerador igual a 0.

   

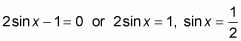
   Si el numerador es igual a 0, entonces toda la fracción es igual a 0. El denominador no debe permitirse para igualar 0 - no existe tal número.

6. Resuelva para los valores de X que satisfacen la ecuación original.

   

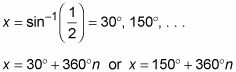
En el siguiente ejemplo, dos ángulos diferentes están en juego. Un ángulo es dos veces el tamaño de la otra, por lo que utilizar una identidad de doble ángulo para reducir los términos de las funciones de un solo ángulo. El truco está en elegir la versión correcta de la identidad de doble ángulo coseno.

Resolver cos 2X + cos X + 1 = 0 para X entre 0 y 2# 112-.

1. Reemplazar cos 2X con 2cos² X - 1.

   2cos²X - 1 + cos X + 1 = 0

   Esta versión de la identidad de doble ángulo de coseno es preferible porque la otra función trigonométrica en la ecuación ya tiene un coseno en ella.

2. Simplifique la ecuación. Entonces factorizar cos X.

   

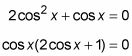
3. Ajuste cada factor igual a 0.

   

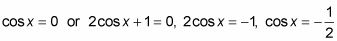
4. Resuelva para los valores de X que satisfacen la ecuación original.

   

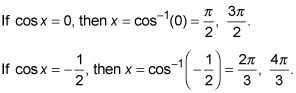
Este último ejemplo puede ser engañosamente simple. El problema es que hay que reconocer una identidad doble ángulo adelantado y hacer un cambio rápido.

1. Utilice la identidad de doble ángulo de seno para crear un cambio para la expresión de la izquierda.

   Comenzando con la identidad y multiplicando cada lado por medio, se obtiene

   

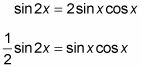
2. Vuelva a colocar la expresión de la izquierda de la ecuación original con su equivalente de la identidad de doble ángulo.

   

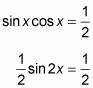
3. Multiplica cada lado de la ecuación por 2.

   

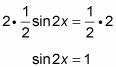
4. Vuelva a escribir la expresión como una función inversa.

   2X = Sen^-1(1)

5. Determine qué ángulos dentro de dos rotaciones satisfacen la expresión.

   2X = Sen^-1(1) = 90 # 176-, 450 # 176;

   Utiliza dos rotaciones ya que el coeficiente de X es 2.

6. Divida cada término por 2.

   

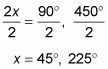
   Observe que los ángulos resultantes son entre 0 y 360 grados.

Usted puede generalizar la técnica del doble ángulo desde el ejemplo anterior para otras expresiones de múltiples ángulos.