Cómo factorizar expresiones trigonométricas con títulos superiores a 2

categoría Educación y lenguas / Matemáticas / Trigonometría

Aunque factoring cuadráticas es una brisa, factoring ecuaciones de trigonometría con grados más altos pueden ser un poco desagradable si usted no tiene una situación agradable, como sólo dos términos o una ecuación de segundo grado similar. A continuación, verá dos de tales problemas: 2sin3 X = Sen X y 2cos4 X - 9cos2 X + 4 = 0.

La primera ecuación tiene sólo dos términos, por lo que puede factorizar por la búsqueda de un mayor factor común. Resuelva 2sin3 X = Sen X para todos los posibles ángulos en grados.

  1. Mueva el término de la derecha a la izquierda de restarlo de cada lado.

    2sin3 X - pecado X = 0

  2. Factorizar el pecado X.

    pecado X (2sin2 X - 1 = 0)

  3. Ajuste cada factor igual a 0.

    pecado X = 0 o 2sin2 X - 1 = 0

  4. Resuelva las dos ecuaciones para los valores de X que satisfacen ellos.

    Si el pecado X = 0, entonces X = Sen-1(0) = 0 °, 180 °,. . . o 0 ° + 180 °n.

    Si 2sin2 X - 1 = 0, 2sin2 X = 1, el pecado2 X = 1/2, entonces usted termina con una ecuación de segundo grado.

  5. Toma la raíz cuadrada de ambos lados de la ecuación de segundo grado y resuelve para X.

    Multiplicar las dos partes de la fracción por el denominador para obtener el radical del denominador.

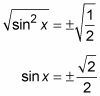
    image0.jpg

    Ahora, teniendo en cuenta las dos soluciones:

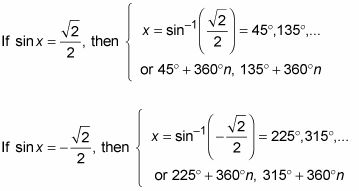
    image1.jpg

Esta ecuación trigonométrica cuarto grado tiene una gran cantidad de respuestas:

X = 180 °n

X = 45 ° + 360 °n

X = 135 ° + 360 °n

X = 225 ° + 360 °n

X = 315 ° + 360 °n

Puede combinar estos últimos cuatro ecuaciones para X, los que comienzan con múltiplos de 45 grados, para leer X = 45 ° + 90 °n. Esta ecuación genera todos los mismos ángulos que los últimos cuatro estados combinados. ¿Cómo sabe usted puede simplificar de esta manera? Debido a que los ángulos de 45, 135, 225, y 315 grados son los 90 grados de separación en valor. Al comenzar con la 45 y la adición de 90 y otra vez, usted obtiene todos los ángulos que cotizan en bolsa, así como el número infinito de sus múltiplos.

El siguiente ejemplo es también una ecuación de cuarto grado, pero éste es cuadrática como, lo que significa que factores como un trinomio de segundo grado en dos factores binomiales. Este problema tiene la posibilidad de tener un gran número de soluciones - o ninguno. Resuelva 2cos4 X - 9cos2 X + 4 = 0 para las soluciones que se encuentran entre 0 y 2pi-.

  1. Factorizar el trinomio como el producto de dos binomios.

    (2cos2 X - 1) (cos2 X - 4) = 0

  2. Ajuste cada factor igual a 0.

    2cos2 X - 1 = 0 o cos2 X - 4 = 0

  3. Resolver para la función en cada ecuación por conseguir con los términos de coseno en ellos por sí solo en un lado de la ecuación.

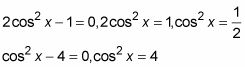
    image2.jpg

  4. Toma la raíz cuadrada de cada lado de cada ecuación.

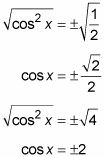
    image3.jpg

  5. Resuelva para los valores de X que satisfacen las ecuaciones.

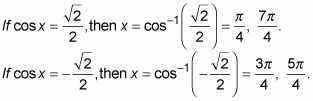
    image4.jpg

    Si cos X = ± 2, entonces usted tiene un problema - que la ecuación no computa! Los resultados de la función coseno solamente en valores entre -1 y 1. Este factor no da nuevas soluciones al problema original.



Artículos Relacionados

Sobre el autor
¿Cómo combinar los ángulos de referencia con otras técnicas para resolver ecuaciones trigonométricas ¿Cómo combinar los ángulos de referencia con otras técnicas para resolver ecuaciones trigonométricas

Puede incorporar ángulos de referencia en algunas otras técnicas de pre-cálculo para resolver ecuaciones trigonométricas. Una de estas técnicas es el factoring. Usted ha estado factoring desde álgebra, por lo que este proceso no debe ser nada…

¿Cómo resolver (y el factor) una ecuación cuadrática con la fórmula cuadrática ¿Cómo resolver (y el factor) una ecuación cuadrática con la fórmula cuadrática

Una ecuación cuadrática es cualquier segundo grado ecuación polinómica - que es cuando la mayor potencia de X, o cualquier otra variable se usa, es de 2. La solución o soluciones de una ecuación de segundo grado,Resolver la ecuación,con la…

¿Cómo resolver una ecuación cuadrática completando el cuadrado ¿Cómo resolver una ecuación cuadrática completando el cuadrado

Puede resolver ecuaciones de segundo grado por completando el cuadrado. Completando la plaza implica la creación de un trinomio cuadrado perfecto de la ecuación de segundo grado, y luego resolver ese trinomio mediante la adopción de su raíz…

Cómo factorizar expresiones trigonométricas por agrupación Cómo factorizar expresiones trigonométricas por agrupación

El proceso de factoring mediante la agrupación de las obras en casos muy especiales, cuando la expresión trigonometría original es el resultado de multiplicar dos binomios juntos que tienen algunos términos no relacionados en ellos.…

¿Cómo encontrar una solución a una ecuación trigonométrica de múltiples ángulos ¿Cómo encontrar una solución a una ecuación trigonométrica de múltiples ángulos

Expresiones trigonometría múltiple de ángulo son aquellos en los que la medida del ángulo es algún múltiplo de una variable - por ejemplo, 2X o 3y. Usted puede tomar estas expresiones separadas y despejar todas las soluciones adicionales que…

Cómo multiplicar a través de una ecuación trigonométrica con otra función Cómo multiplicar a través de una ecuación trigonométrica con otra función

La técnica de multiplicar a través de una ecuación de trigonometría por una función selecta no debe ser su primera opción - o su segunda, tercera o cuarta opción. Este método suele ser el último recurso. No es que el método es…

¿Cómo resolver una ecuación de trigonometría utilizando la fórmula cuadrática ¿Cómo resolver una ecuación de trigonometría utilizando la fórmula cuadrática

Cuando el factor trigonometría ecuaciones de segundo grado, la vida es buena. Cuando no lo hacen, usted todavía puede sobrevivir, gracias a que la fórmula cuadrática maravilloso. En caso de que hayas olvidado la fórmula exacta, aquí está.La…

¿Cómo resolver una ecuación de trigonometría factorizando cuadráticas ¿Cómo resolver una ecuación de trigonometría factorizando cuadráticas

Ecuaciones cuadráticas son agradables de trabajar porque, cuando no factor, puede resolverlos mediante el uso de la fórmula cuadrática. Los tipos de ecuaciones trigonométricas cuadráticas que puede factores son los que, como bronceado2 X = Tan…

¿Cómo resolver una ecuación trigonométrica que tiene múltiples funciones trigonométricas ¿Cómo resolver una ecuación trigonométrica que tiene múltiples funciones trigonométricas

Algunas ecuaciones de trigonometría contienen más de una función trigonométrica. Otros tienen mezclas de múltiples ángulos y ángulos individuales con la misma variable. Algunos ejemplos de tales ecuaciones incluyen 3cos2 X = Sen2 X, 2 seg X =…

Cómo cuadrar ambos lados de una ecuación trigonométrica Cómo cuadrar ambos lados de una ecuación trigonométrica

Cuando la resolución de ecuaciones de trigonometría, más de un método generalmente funciona - a pesar de un método es a menudo más rápido o más fácil que otro. Con la práctica, usted obtendrá buenos en la elección de la mejor de las…

La identificación de propiedades algebraicas más utilizados en la resolución de identidades La identificación de propiedades algebraicas más utilizados en la resolución de identidades

Resolución de identidades es casi un rito de paso para los que estudian trigonometría. Hacer frente a la perspectiva de la resolución de identidades - y más tarde simplificar expresiones trigonométricas en cálculo - va mucho más suavemente si…

Vuelve a escribir una ecuación de trigonometría simple utilizando un inverso para resolverlo Vuelve a escribir una ecuación de trigonometría simple utilizando un inverso para resolverlo

El tipo más simple de la ecuación de trigonometría es el que puede volver a escribir de inmediato como una inversa con el fin de determinar las soluciones. Algunos ejemplos de estos tipos de ecuaciones incluyen:Para resolver cos X = 1, siga estos…

» » » » Cómo factorizar expresiones trigonométricas con títulos superiores a 2