Desenterrar raíces polinómicas con factoring
Al resolver las raíces (X
-intercepciones de un polinomio), que en general tienen que factorizar la regla de la función y la puso igual a 0. La factorización puede ser simple y obvia o complicado y oscuro. Siempre esperas por el simple y obvio, traslado a un reto y factible, y recurrir a la " grandes armas " cuando los factores son más oscuros.Antes de ir a esas longitudes, sin embargo, usted tiene que agotar otros métodos. Los otros métodos de factoring incluyen
Dividiendo un máximo común divisor (MCD)
Factoring un binomio cuadrado perfecto
Factoring por agrupación
Factoring trinomios cuadrática similares
Ejemplos de preguntas
Encuentra las raíces (soluciones) del polinomio X7 - 82X5 + 81X3 = 0.
X= 0, 0, 0, 9, -9, 1, -1. Esta ecuación técnicamente tiene siete soluciones, pero el 0 es una raíz múltiple, por lo que terminan con sólo cinco números diferentes. Para encontrar estas soluciones, es primer factor X3 de cada término para obtener X3(X4 - 82X2 + 81) =
Los dos binomios son a la vez la diferencia de cuadrados perfectos, para que pueda tenerlas en cuenta en la diferencia y la suma de las raíces de los términos. Usted obtiene X3(X - 9) (X + 9) (X - 1) (X + 1) = 0. Ajuste cada uno de los factores iguales a 0, a encontrar las raíces.
Encuentra las raíces (soluciones) del polinomio X3 - 16X2 + 100X - 1600 = 0.
X = 16. El polinomio no tiene un factor común en los cuatro términos, pero se puede agrupar los términos para los pares de factores comunes. Usted obtiene X2(X - 16) + 100 (X - 16) = 0, que factores en (X - 16)(X2 + 100) = 0. El segundo binomial es la suma de los cuadrados, que no factor.
La configuración de estos dos factores iguales a 0, se obtiene X = 16 desde el primer factor, pero el segundo factor no produce ninguna respuesta reales. A pesar de que comenzó con un polinomio de tercer grado, que puede producir hasta tres soluciones, este polinomio tiene una sola raíz real. La solución es sólo X = 16.
Preguntas de práctica
Encuentra las raíces (soluciones) del polinomio 3X4 - 12X3 - 27X2 + 108X = 0.
Encuentra las raíces (soluciones) del polinomio X5 - 16X3 + X2 - 16 = 0.
Encuentra las raíces (soluciones) del polinomio X6 + 9X3 + 8 = 0.
Encuentra las raíces (soluciones) del polinomio 36X5 - 13X3 + X = 0.
A continuación se presentan las respuestas a las preguntas de la práctica:
La respuesta es X= 0, 3, -3, 4.
En primer lugar el factor 3X de cada término para obtener 3X(X3 - 4X2 - 9X + 36) = 0. A continuación, puede factorizar los términos entre paréntesis mediante la agrupación: 3X[X2(X - 4) -9 (X - 4)] = 3X[(X - 4) (X2 - 9)] = 3X[(X - 4) (X - 3) (X + 3)] = 0. Set cada factor igual a 0 para resolver para las raíces.
La respuesta es X= 4, -4, -1.
Los factores del polinomio por agrupación: X3(X2 - 16) + 1 (X2 - 16) = (X2 - 16)(X3 + 1) = (X - 4) (X + 4) (X + 1) (X2 - X + 1) = 0. Los tres primeros factores que dan las raíces reales. El último factor es una cuadrática que no tiene solución real cuando lo establece igual a 0.
Usted realmente no tiene un factor X3 + 1 en el problema 6 para encontrar la raíz. Si usted acaba de configurar X3 + 1 igual a 0, se obtiene X3 = -1, Y tomando la raíz cúbica de ambos lados le da la solución -1. La forma factorizada simplemente te muestra cómo este problema podría haber tenido cinco raíces, pero no todos son números reales en este caso.
La respuesta es X= -2, -1.
El polinomio es cuadrática similares. Es factores en (X3 + 8) (X3 + 1) = 0. Ajuste cada factor igual a 0, se obtiene las dos raíces.
La respuesta es
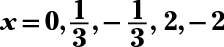
En primer lugar, el factor X de cada término para obtener X(36X4 - 13X2 + 1) = 0. Los factores trinomio cuadrático-como, que le da X(9X2 - 1) (4X2 - 1) = 0. Cada binomial es la diferencia de los cuadrados, por lo tanto el factor binomios. Para la factorización final, usted termina con X(3X - 1) (3X + 1) (2X - 1) (2X + 1) = 0. Ajuste cada factor igual a 0 le da las cinco soluciones diferentes.
Conceptos básicos de cómo adivinar y comprobar raíces reales Puede utilizar el teorema de la raíz racional para restringir la búsqueda de las raíces de los polinomios. Si bien la regla de los signos de Descartes sólo se estrecha hacia abajo las raíces reales en positivo y negativo, el teorema de la raíz…
Factoring cuatro o más términos agrupando Cuando un polinomio tiene cuatro o más términos, la forma más fácil de factorizar que es usar agrupación. En este método, nos fijamos en sólo dos términos a la vez para ver si cualquiera de las técnicas se hacen evidentes. Por ejemplo,…
Encontrar las raíces de una ecuación factorizada En pre-cálculo, puede utilizar la propiedad del producto cero a encontrar las raíces de una ecuación factorizada. Después se toma un polinomio en sus diferentes piezas, puede configurar cada pieza igual a cero para resolver las raíces con la…
Cómo romper una diferencia cúbica o la suma Después de que se haya registrado para ver si hay un máximo común divisor (MCD) de un polinomio dado y descubrió que es un binomio que no es una diferencia de cuadrados, se debe considerar que puede ser una diferencia o suma de cubos.LA…
Cómo factorizar expresiones matemáticas A menudo se necesita factor expresiones (rompen esas expresiones en sus componentes más simples, o factores) Para el cálculo. Medios de factoring " unmultiplying, " como la reescritura de 12 comoNo encuentras con problemas como que en el cálculo,…
Cómo factorizar una expresión polinómica En matemáticas, factorización o factorización es la ruptura aparte de un polinomio en un producto de polinomios otros más pequeños. Si lo desea, usted podría entonces multiplicar estos factores juntos, y usted debe obtener el polinomio…
¿Cómo encontrar un factor común más grande de un polinomio No importa cuántos términos de un polinomio tiene, uno siempre quiere comprobar si hay un máximo común divisor (MCD) en primer lugar. Si el polinomio tiene un GCF, factoring el resto del polinomio es mucho más fácil porque una vez que se toma…
¿Cómo encontrar raíces imaginarias usando el teorema fundamental del álgebra El teorema fundamental del álgebra puede ayudarle a encontrar las raíces imaginarias. Raíces imaginarias aparecerá en una ecuación de segundo grado cuando el discriminante de la ecuación de segundo grado - la parte bajo el signo de la raíz…
¿Cómo encontrar las raíces reales de un polinomio utilizando la regla de los signos de Descartes Si sabe el número de raíces totales un polinomio tiene, puede utilizar un teorema muy bien llamada Regla de los signos de Descartes a contar cuántas raíces son números reales (tanto positivos y negativa) y cuántos son imaginarios. Usted ve, el…
Cómo graficar polinomios cuando las raíces son números imaginarios - una visión general En pre-cálculo y en el cálculo, ciertas funciones polinómicas tener raíces no reales además de raíces reales (y algunas de las funciones más complicadas tener todas raíces imaginarias). Cuando usted debe encontrar tanto, empezar por la…
¿Cómo adivinar y comprobar raíces reales - 1 - lista de todas las posibles raíces racionales Cuando usted busca todo lo posible raíces racionales de cualquier polinomio, el primer paso es utilizar el teorema de la raíz racional para mencionarlos a todos.El teorema de la raíz racional dice que si usted toma todos los factores de la…
¿Cómo resolver (y el factor) una ecuación cuadrática con la fórmula cuadrática Una ecuación cuadrática es cualquier segundo grado ecuación polinómica - que es cuando la mayor potencia de X, o cualquier otra variable se usa, es de 2. La solución o soluciones de una ecuación de segundo grado,Resolver la ecuación,con la…