Cómo factorizar una expresión polinómica

En matemáticas, factorización

o factorización es la ruptura aparte de un polinomio en un producto de polinomios otros más pequeños. Si lo desea, usted podría entonces multiplicar estos factores juntos, y usted debe obtener el polinomio original, (esta es una gran manera de comprobar usted mismo en sus habilidades de factoring). Un conjunto de factores, por ejemplo, de los 24 es de 6 y 4, ya 6 veces 4 = 24. Cuando tienes un polinomio, una manera de resolverlo es factorizar en el producto de dos binomios.

Tiene varias opciones de factoraje para elegir al resolver ecuaciones polinómicas:

• Para un polinomio, no importa cuántos términos que tiene, siempre comprobar si hay una máximo común divisor (GCF) primero. Literalmente, el mayor factor común es la expresión más grande que voy a entrar en todos los términos. Utilizando el GCF es como hacer la propiedad distributiva hacia atrás.

• Si la ecuación es una trinomio - tiene tres términos - se puede utilizar el método FOIL para multiplicar binomios hacia atrás.

• Si se trata de un binomio, busque diferencia de cuadrados, diferencia de cubos, o la suma de los cubos.

Finalmente, después de que el polinomio está completamente factorizado, puede utilizar la propiedad del producto cero para resolver la ecuación.

Si un polinomio no tiene en cuenta, se llama primo porque sus únicos factores son 1 y sí mismo. Cuando usted ha intentado todos los trucos de factoraje en su bolsa (GCF, hacia atrás FOIL, diferencia de cuadrados, y así sucesivamente), y la ecuación cuadrática no los factores, entonces usted puede o bien completar el cuadrado o usar la fórmula cuadrática para resolver la ecuación . La decisión es tuya. Usted podría incluso potencialmente optar por utilizar siempre ya sea completando la fórmula cuadrada o cuadrática (y saltar el factoring) para resolver una ecuación. Factoring a veces puede ser más rápido, por lo que se recomienda que lo pruebe primero.

Formulario estándar para una expresión cuadrática (simplemente una ecuación de segundo grado sin el signo igual) es la X-término al cuadrado, seguido por el X plazo, seguido por la constante - en otras palabras,

Si te dan una expresión cuadrática que no está en forma estándar, reescribirla en forma estándar, poniendo los grados en orden descendente. Esto hace que el factoring más fácil (y es a veces incluso necesario de los factores).

Siempre el primer paso: Busque un GCF

No importa cuántos términos de un polinomio tiene, siempre es importante consultar para un máximo común divisor (MCD) en primer lugar. Si hay un marco de cooperación mundial, que hará que factorizar el polinomio mucho más fácil debido a que el número de factores de cada término será menor (ya que se han factorizado uno o más de ellos fuera!). Esto es especialmente importante si el GCF incluye una variable.

Si se olvida de factorizar este GCF, también te olvides de encontrar una solución, y que podría mezclar que en más de un sentido! Sin esa solución, se puede perder una raíz, y entonces usted podría terminar con un gráfico incorrecto para su polinomio.

Para factorizar el polinomio

por ejemplo, siga estos pasos:

1. Divida cada término en factores primos.

   Esto expande la expresión de

   

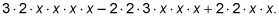
2. Puedes buscar los factores que aparecen en cada plazo para determinar el GCF.

   En este ejemplo, se puede ver uno 2 y dos X's en cada término. Estos están subrayadas en la siguiente:

   

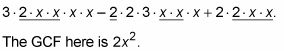
3. Factor del GCF hacia fuera de cada término en frente de paréntesis, y dejar los restos en el interior de los paréntesis.

   Ahora tiene

   

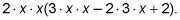
4. Multiplique a cabo para simplificar cada término.

   Esto le da

   

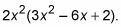
5. Distribuir a asegurarse de que el GCF es correcta.

   

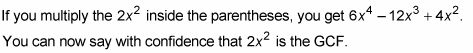
Envuelva para arriba: El método FOIL para trinomios

Después de que se haya registrado un polinomio por un GCF (independientemente de si tenía uno o no), trate al factor nuevo. Usted puede encontrar que es más fácil que factor después de la formación bruta de capital ha sido un factor fuera. El polinomio anterior tenía dos factores:

Sin embargo, el segundo factor puede ser capaz de factorizar nuevo porque es un trinomio, y si lo hace usted tendrá dos factores más que son los dos binomios.

La mayoría de los profesores muestran el método de estimación y comprobación de factoring, donde anotar dos conjuntos de paréntesis;

- y enchufe, literalmente, en conjeturas de los factores para ver si algo funciona. Tal vez su primera conjetura para este ejemplo sería (3X - 2) (X - 1), pero si se frustró esto, se llega a

y usted tendría que adivinar de nuevo. Este método conjetura-y-cheque es looooooong y tedioso, en el mejor. De hecho, este cuadrática particular es primo, por lo que podría adivinar y comprobar todo el día y sería nunca factor.

Si usted está en pre-cálculo y su profesor está utilizando el método de estimación y comprobación de factoring, que simplemente no está funcionando para ti, has llegado a la sección de la derecha. En el siguiente procedimiento, llamado el Método FOIL de factoring (a veces llamado el Método británica), Siempre funciona para factorizar trinomios y es una herramienta muy útil si no se puede envolver su cerebro alrededor de conjetura y verificación. Cuando el método FOIL falla, usted sabe a ciencia cierta la cuadrática dado es primo.

El método FOIL de factoring llama para que usted siga los pasos necesarios para frustrar binomios, sólo que al revés. Recuerde que cuando usted Foil, se multiplica la primera fuera, dentro, y el último término, juntos. Entonces usted combina cualquier términos semejantes, que generalmente provienen de la multiplicación de los Outer y condiciones internas.

Por ejemplo, al factor

sigue estos pasos:

1. Compruebe que el GCF primero.

   la expresión

   

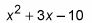
   no tendrá GCF cuando se descomponen y se mire, de acuerdo a los pasos de la sección anterior. El desglose se ve así:

   

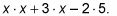
   No hay factores que son comunes a cada término, así que no hay GCF. Eso significa que se llega a pasar a la siguiente etapa.

2. Multiplique el término cuadrático y el término constante.

   Tenga cuidado con los signos cuando usted hace esto. En este ejemplo, el término cuadrático es

   

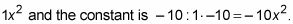
3. Anote todos los factores del resultado, de dos en dos.

   

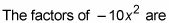
4. -1X y 10X

5. 1X y -10X

6. -2X y 5X

7. 2X y -5X

8. De esta lista, encontrar el par que se suma para producir el coeficiente del término lineal.

   Usted quiere que el par cuya suma es 3X. Para este problema, la respuesta es-2X y 5X porque

   

9. Romper el término lineal en dos términos, utilizando los números de la Etapa 4 como los coeficientes.

   Escrito a cabo, ahora tiene

   

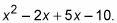
   Se hace la vida más fácil en el largo plazo si siempre organizar el término lineal con el coeficiente más pequeño primero. Es por eso que se pone el -2X en frente de la 5X.

10. Grupo de los cuatro términos en dos grupos de dos.

    Siempre ponga un signo más entre los dos conjuntos:

    

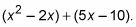
11. Encuentra el MCD de cada conjunto y el factor a cabo.

    Mira los dos primeros términos. ¿Qué tienen en común? Un X. Si se toma el X, Tienes X(X - 2). Ahora, mira a los dos segundos términos. Comparten un 5. Si se toma la 5, que tiene 5 (X - 2). El polinomio se escribe ahora como X(X - 2) + 5 (X - 2).

12. Encuentra el MCD de los dos nuevos términos.

    ¿Ves la (X - 2) en ambos términos? Están subrayados aquí: X(X - 2) + 5(X - 2). Eso es un GCF porque aparece en ambos términos (si se toma con este método, el último paso siempre debe tener este aspecto). Factorizar el MCD de ambos términos (que es siempre la expresión entre paréntesis) a la delantera que te dan (X - 2) (). Cuando se toma hacia fuera, los términos que no son el GCF se quedan dentro de las nuevas paréntesis. En este caso, se obtiene (X - 2) (X + 5). Los (X + 5) es el sobrante de quitarle el GCF.

A veces, la señal tiene que cambiar en el Paso 6 para factorizar correctamente el GCF. Pero si usted no comienza con un signo más entre los dos conjuntos, puede perder un signo negativo que necesita un factor hasta el final. Por ejemplo, en la factorización

usted termina en el paso 5 con el siguiente polinomio:

Factorizar el X en el primer set y el 4 en el segundo set para conseguir X(X - 9) + 4 (-X + 9). Observe que el segundo conjunto es exactamente lo contrario de la primera? Para que usted se mueva a la siguiente etapa, los juegos tienen que coincidir exactamente. Para solucionar este problema, cambie el 4 en el medio a -4 y obtener X(X - 9) - 4 (X - 9). Ahora que coinciden, se puede factorizar nuevo.

Si sigues todos los pasos en la lista anterior, tendrá un tiempo fácil con trinomios factoraje. Incluso cuando una expresión tiene un coeficiente de liderazgo, además de 1, el método FOIL todavía funciona. La llave inglesa viene sólo si no hay factores en el Paso 2 que se suman para darle el coeficiente lineal. En este caso, la respuesta es primo.