Simplificar y factorizar expresiones
En álgebra, la simplificación y factoring expresiones son procesos opuestos. Simplificar una expresión
a menudo significa eliminación un par de parentheses- factorizar una expresión a menudo significa aplicar ellos.Supongamos que comienza con la expresión 5X(2X2 - 3X + 7). Para simplificar esta expresión, se quita los paréntesis multiplicando 5X por cada uno de los tres términos dentro de los paréntesis:
= 10X3 - 15X2 + 35X
Usted puede factorizar la expresión resultante mediante la sustitución de los paréntesis: Simplemente dividir cada término en un factor de 5X:
5X(2X2 - 3X + 7)
Las dos formas de esta expresión - 5X(2X2 - 3X + 7) y 10X2 - 15X2 + 35X - son equivalentes. Ninguna forma es mejor que el otro. Pero, dependiendo de las circunstancias, una forma puede ser más útil.
Simplificar expresiones desordenadas
Puede usar la simplificación de limpiar expresiones desordenadas y que sean más fáciles de trabajar. Supongamos que usted está trabajando con la siguiente expresión:
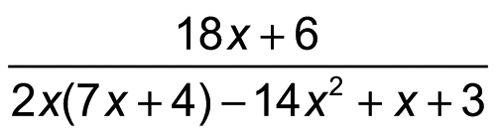
Para limpiarlo, empezar por simplificar el denominador:
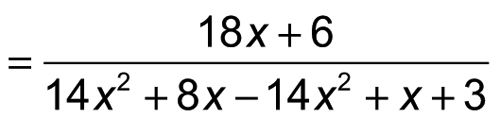
Entonces usted combina los términos semejantes en el aviso denominator- que el X2 términos se anulan entre sí.
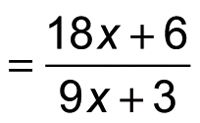
Esta fracción se parece mucho más simple, pero se puede simplificar aún más al factorizar el numerador y denominador:
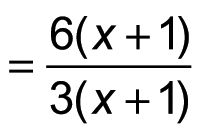
Ahora se puede cancelar un factor de X + 1 y simplificar la fracción resultante de la siguiente manera:
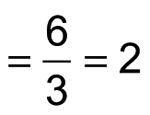
A través de una combinación de simplificación y de factoring, la expresión de aspecto complicado resulta ser un muy simple constante!
Factoring polinomios de segundo grado
Factoring puede ser difícil, especialmente cuando se necesita para factorizar un polinomio con coeficientes grandes, como 15X2 + 47 - 10. Aquí está una manera fácil de factorizar polinomios de segundo grado de la forma laX2 + bX + c:
Comienza dibujando una gran X, colocando el valor ac en el cuadrante superior y b en el cuadrante inferior.
Suponga que desea factorizar el polinomio 6X2 + 11X + 4. Tenga en cuenta que, en este polinomio, la = 6, b = 11, y c = 4. En este problema, ac = 6x4 = 24 y b = 11.
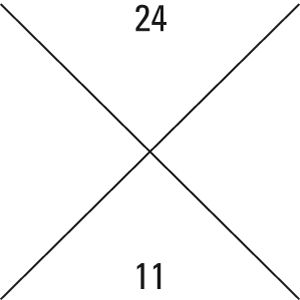
Encontrar un par de números que multiplicar al número de arriba y añadir al número de abajo, y colocarlos en los dos cuadrantes laterales (el orden no importa).
Por ejemplo, usted quiere encontrar un par de números que se multiplica a 24 y se suma a 14. Comience haciendo una lista de todos los pares de factores de 24: 1x24, 2x12, 3x8 y 4x6. Observe que 3 + 8 = 11, por lo que este es el par correcto de los números.
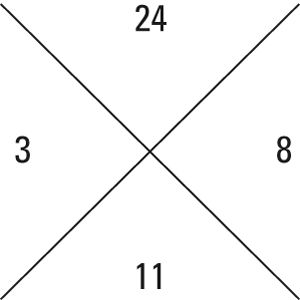
Haga dos fracciones usando hacha para el numerador y los dos números que colocó en los cuadrantes laterales como denominadores.
Aquí, el valor hacha = 6X, y los números en los dos cuadrantes laterales son 3 y 8:
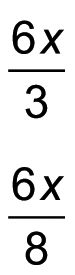
Reducir estas dos fracciones a su mínima expresión (manteniendo los resultados tanto con un numerador y el denominador).
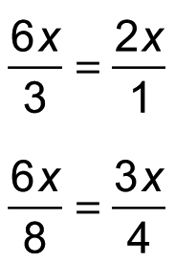
Para terminar, añadir el numerador y el denominador de cada fracción para encontrar los dos factores del polinomio inicial.
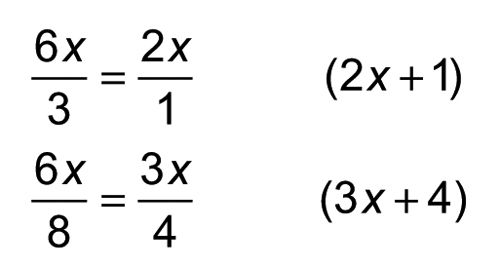
Por lo tanto, 6X2 + 11 + 4 = (2X + 1) (3X + 4)
Ahora, trata el mismo método en el más difícil polinómica 15X2 + 47X - 10. En este caso, la = 15, b = 47, y c = -10.
Comienza dibujando una gran X, colocando el valor ac en el cuadrante superior y b en el cuadrante inferior.
En este problema, ac = 15 x = -10 -150 y b = 47.
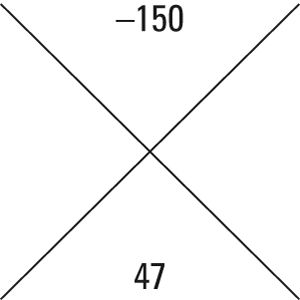
Encontrar un par de números que multiplicar al número de arriba y añadir al número de abajo, y colocarlos en los dos cuadrantes laterales (el orden no importa).
Usted está buscando un par de números que se multiplican a -150, por lo que un número es positivo y el otro es negativo. Y estos dos números también se suman a 47, por lo que el número positivo es el "más grande" de los dos números.
Por lo tanto, aquí están los pares de factores que funcionan: -1x150, -2x75, -3x50, -5x30, -6x25 y -10x15. Observe que -3 + 50 = 47, por lo que este es el par correcto de los números.
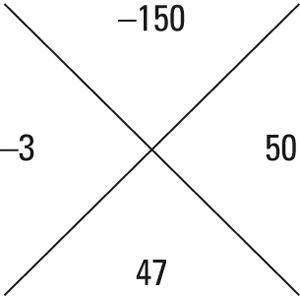
Haga dos fracciones usando hacha para el numerador y los dos números que colocó en los cuadrantes laterales como denominadores.
Aquí, el valor hacha = 15X, y los números en los dos cuadrantes laterales son -3 y 50:
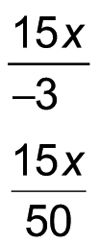
Reducir estas dos fracciones a su mínima expresión (manteniendo los resultados tanto con un numerador y el denominador).
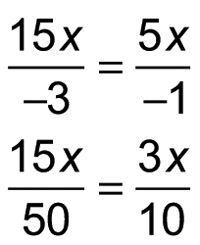
Para terminar, añadir el numerador y el denominador de cada fracción para encontrar los dos factores del polinomio inicial.
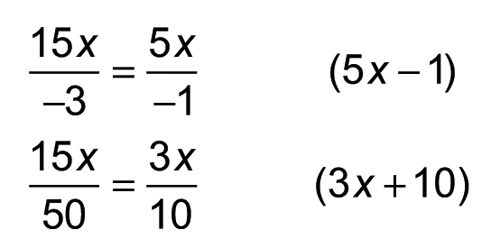
Por lo tanto, 15X2 + 47X - 10 = (5X - 1) (3X + 10).
Consejos de matemáticas básicas: fracciones Las fracciones son una forma común de describir partes de un todo. Se utilizan comúnmente para los pesos y medidas en inglés, especialmente para las pequeñas medidas en la cocina y la carpintería. Si quieres ser competentes en matemáticas…
Cómo convertir de porcentajes a fracciones La conversión de los porcentajes de las fracciones es bastante sencillo. Recuerde que la palabra por ciento medio " sobre 100. " Así que el cambio de porcentajes a fracciones, naturalmente, implica el número 100.Para convertir un porcentaje a una…
¿Cómo encontrar la suma de fracciones con el mismo denominador Al agregar dos fracciones que tienen el mismo denominador (número inferior), sólo tiene que añadir los numeradores (arriba números) juntos y dejar el denominador sin cambios.Por ejemplo, consideremos el siguiente problema:Como se puede ver,…
¿Cómo aumentar los términos de una fracción Incluso si se ven diferentes fracciones, que en realidad puede representar la misma cantidad- en otras palabras, una de las fracciones habrá aumentado términos en comparación con el otro. Puede que tenga que aumentar los términos de las…
Cómo aumentar y reducir los términos de las fracciones Al cortar un pastel en dos pedazos y tomar una sola pieza, que tiene un medio de la torta. Y cuando se corta en cuatro trozos y tomar dos, usted tiene 2/4 de la torta. Por último, cuando se corta en seis pedazos y tomar tres, usted tiene 3/6 de la…
Cómo multiplicar dos fracciones y reducir la respuesta Para multiplicar dos fracciones, es necesario tener un conocimiento básico de las tablas de multiplicar y la capacidad de reducir la respuesta a su mínima expresión.Multiplica los numeradores (los números en la parte superior) en conjunto para…
Cómo multiplicar fracciones ¿Por qué no todo en la vida ser tan fácil como la multiplicación de fracciones? Para multiplicar dos fracciones, simplemente hacer lo siguiente: Multiplique los dos numeradores (números superiores) para obtener el numerador de la respuesta-…
Cómo reducir una fracción a su mínima expresión Incluso si se ven diferentes fracciones, que en realidad puede representar la misma cantidad- en otras palabras, una de las fracciones habrá reducido términos en comparación con el otro. Puede que tenga que reducir los términos de las fracciones…
¿Cómo distinguir expresiones racionales propias e impropias Integración por fracciones parciales sólo funciona con expresiones racionales adecuadas, pero no con expresiones racionales impropias. Decirle a una fracción propia a partir de uno inadecuada es fácil: Una fracción a / b es correcta si el…
¿Cómo encontrar un factor común más grande de un polinomio No importa cuántos términos de un polinomio tiene, uno siempre quiere comprobar si hay un máximo común divisor (MCD) en primer lugar. Si el polinomio tiene un GCF, factoring el resto del polinomio es mucho más fácil porque una vez que se toma…
¿Cómo encontrar el límite de una función algebraica Cuando su profesor de pre-cálculo le pide que encontrar el límite de una función algebraica, usted tiene cuatro técnicas para elegir: enchufar el X valor, el factoring, racionalizar el numerador, y encontrar el mínimo común denominador.El…
Cómo simplificar expresiones trigonométricas con un binomio en el denominador de una fracción Cuando una expresión trigonométrica es una fracción con un binomio en su denominador, siempre tenga en cuenta multiplicando por el conjugado antes de hacer cualquier otra cosa. La mayoría de las veces, esta técnica permite simplificar.Por…