Cómo aumentar y reducir los términos de las fracciones
Al cortar un pastel en dos pedazos y tomar una sola pieza, que tiene un medio de la torta. Y cuando se corta en cuatro trozos y tomar dos, usted tiene 2/4 de la torta. Por último, cuando se corta en seis pedazos y tomar tres, usted tiene 3/6 de la torta. Observe que en todos estos casos, se obtiene la misma cantidad de pastel.
Esto muestra que las fracciones 1/2, 2/4 y 3/6 son igualdad también lo son las fracciones 10/20 y
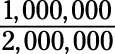
La mayoría del tiempo, escribiendo esta fracción como media se prefiere debido a que el numerador y el denominador son los más pequeños números posibles. En otras palabras, la fracción media está escrito en su mínima expresión. Al final de un problema, a menudo es necesario reducir una fracción, o escribirlo en su mínima expresión. Hay dos maneras de hacer esto - la manera informal y de la manera formal:
La manera informal para reducir una fracción es dividir el numerador y el denominador por el mismo número.
Ventaja: La manera informal es fácil.
Desventaja: No siempre reducir la fracción a su mínima expresión (aunque lo hace llegar la fracción en su mínima expresión si se divide por el máximo común divisor).
La manera formal es descomponer el numerador y el denominador en sus factores primos y luego cancelar factores comunes.
Ventaja: La manera formal siempre reduce la fracción a su mínima expresión.
Desventaja: Se necesita más tiempo que el modo informal.
Comience cada problema con la manera informal. Si las cosas se ponen difíciles y todavía no está seguro de si su respuesta se reduce a su mínima expresión, cambiar a la manera formal.
A veces, al comienzo de un problema de fracciones, es necesario aumentar los términos de una fracción - es decir, escribir esa fracción utilizando un mayor numerador y denominador. Para aumentar términos, multiplicar el numerador y el denominador por el mismo número.
Ejemplos de preguntas
Aumentar los términos de la fracción 4/5 a una nueva fracción cuyo denominador es 15:
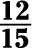
Para empezar, escribir el problema de la siguiente manera:
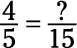
El signo de interrogación significa el numerador de la nueva fracción, que desea rellenar. Ahora divida el denominador más grande (15) por el denominador más pequeño (5).
15/5 = 3
Multiplique este resultado por el numerador:
3 x 4 = 12
Por último, tome este número y lo utilizan para reemplazar el signo de interrogación:
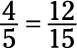
Reducir la fracción 18/42 a su mínima expresión.
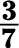
El numerador y el denominador no son demasiado grandes, a fin de utilizar la forma informal: Para empezar, tratan de encontrar un pequeño número que el numerador y el denominador son ambos divisibles por. En este caso, observe que el numerador y el denominador son ambos divisibles por 2, por lo tanto se dividen por 2:
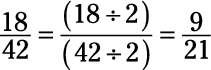
A continuación, observe que el numerador y el denominador son ambos divisibles por 3, por lo tanto se dividen por 3:
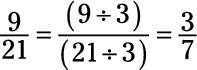
En este momento, no hay ningún número (excepto 1) que divide de manera uniforme tanto en el numerador y el denominador, por lo que esta es su respuesta.
Reducir la fracción 135/196 a su mínima expresión.
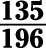
El numerador y el denominador son a la vez más de 100, a fin de utilizar de la manera formal. En primer lugar, descomponer el numerador y el denominador a sus factores primos:
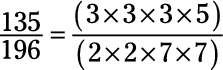
El numerador y el denominador no tienen factores comunes, por lo que la fracción ya en su mínima expresión es.
Preguntas de práctica
Aumentar los términos de la fracción 2.3 para que el denominador es 18.
Aumentar los términos de 4/9, cambiando el denominador a 54.
Reducir la fracción 12/60 a su mínima expresión.
Reducir 45/75 a su mínima expresión.
Reducir la fracción 135/180 a su mínima expresión.
Reducir 108/217 a su mínima expresión.
A continuación se presentan las respuestas a las preguntas de la práctica:
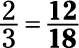
Para empezar, escribir el problema de la siguiente manera:
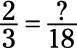
Divida el denominador más grande (18) por el denominador más pequeño (3) y luego multiplicar este resultado por el numerador (2):
6 x 2 = 12
Tome este número y lo utilizan para reemplazar la pregunta marca- su respuesta es
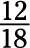
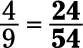
Escriba el problema de la siguiente manera:
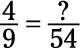
Divida el denominador más grande (54) por el denominador más pequeño (9) y luego multiplicar este resultado por el numerador (4):
6 x 4 = 24
Tome este número y lo utilizan para reemplazar la pregunta marca- su respuesta es
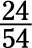
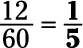
El numerador (12) y el denominador (60) son a la vez, incluso, por lo tanto se dividen por 2:
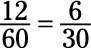
Siguen siendo tanto incluso, por lo que divide ambos por 2 otra vez:
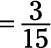
Ahora el numerador y el denominador son ambos divisibles por 3, por lo tanto se dividen por 3:
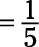
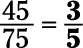
El numerador (45) y el denominador (75) son ambos divisibles por 5, por lo tanto se dividen por 5:
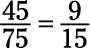
Ahora el numerador y el denominador son ambos divisibles por 3, por lo tanto se dividen por 3:
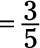
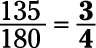
El numerador (135) y el denominador (180) son ambos divisibles por 5, por lo tanto se dividen por 5:
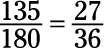
Ahora el numerador y el denominador son ambos divisibles por 3, por lo tanto se dividen por 3:
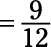
Siguen siendo tanto divisible por 3, por lo tanto se dividen por 3 otra vez:
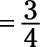
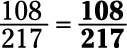
Con un numerador y el denominador de este grande, reducir el uso de la manera formal. En primer lugar, descomponer el numerador y el denominador a sus factores primos:
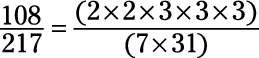
El numerador y el denominador no tienen factores comunes, por lo que la fracción ya en su mínima expresión es.
Cómo convertir entre números mixtos y fracciones impropias Cuando el numerador (número superior) es mayor que el denominador (número inferior), que es una fracción fracción impropia. Una forma alternativa de una fracción impropia es como numero mixto, que se compone de un número entero y una…
Cómo convertir de decimales a fracciones Algunas conversiones de decimales muy comunes a fracciones son fáciles. En otros casos, hay que hacer un poco más de trabajo. Aquí es cómo cambiar cualquier decimal en una fracción:Crear un " fracción " con el decimal en el numerador y 1,0 en…
¿Cómo encontrar la suma de fracciones con el mismo denominador Al agregar dos fracciones que tienen el mismo denominador (número inferior), sólo tiene que añadir los numeradores (arriba números) juntos y dejar el denominador sin cambios.Por ejemplo, consideremos el siguiente problema:Como se puede ver,…
¿Cómo aumentar los términos de una fracción Incluso si se ven diferentes fracciones, que en realidad puede representar la misma cantidad- en otras palabras, una de las fracciones habrá aumentado términos en comparación con el otro. Puede que tenga que aumentar los términos de las…
Cómo multiplicar dos fracciones y reducir la respuesta Para multiplicar dos fracciones, es necesario tener un conocimiento básico de las tablas de multiplicar y la capacidad de reducir la respuesta a su mínima expresión.Multiplica los numeradores (los números en la parte superior) en conjunto para…
Cómo multiplicar fracciones ¿Por qué no todo en la vida ser tan fácil como la multiplicación de fracciones? Para multiplicar dos fracciones, simplemente hacer lo siguiente: Multiplique los dos numeradores (números superiores) para obtener el numerador de la respuesta-…
Cómo reducir una fracción a su mínima expresión Incluso si se ven diferentes fracciones, que en realidad puede representar la misma cantidad- en otras palabras, una de las fracciones habrá reducido términos en comparación con el otro. Puede que tenga que reducir los términos de las fracciones…
Cómo restar fracciones con el mismo denominador Restar fracciones con el mismo denominador (número inferior) es fácil. Cuando los denominadores son los mismos, sólo puede pensar en las fracciones como pedazos de torta.Para restar una fracción de otro cuando ambos tienen el mismo denominador,…
Cómo restar fracciones con denominadores comunes Como con la adición, restando fracciones que tienen el mismo denominador (también llamado común denominador) Es muy simple: sólo resta el segundo numerador de la primera y mantener el denominador de la misma. En algunos casos, es posible que…
¿Cómo distinguir expresiones racionales propias e impropias Integración por fracciones parciales sólo funciona con expresiones racionales adecuadas, pero no con expresiones racionales impropias. Decirle a una fracción propia a partir de uno inadecuada es fácil: Una fracción a / b es correcta si el…
Cómo multiplicar por un conjugado de encontrar una identidad trigonometría Conjugados ofrecen una gran manera de encontrar identidades trigonométricas. En matemáticas, un conjugado formado por los mismos dos términos como la primera expresión, separados por el signo opuesto. Por ejemplo, el conjugado deEn trig,…
Preparación ASVAB: cómo sumar y restar fracciones Adición y sustracción de fracciones para el ASVAB (o para cualquier otro propósito) puede ser tan simple como multiplicar y dividir, o puede ser más difícil. A medida que la siguiente información muestra, todo depende de si las fracciones…