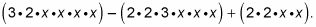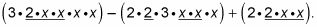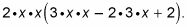¿Cómo encontrar un factor común más grande de un polinomio
No importa cuántos términos de un polinomio tiene, uno siempre quiere comprobar si hay un máximo común divisor (MCD) en primer lugar. Si el polinomio tiene un GCF, factoring el resto del polinomio es mucho más fácil porque una vez que se toma el GCF, los términos restantes serán menos engorroso. Si el MCD incluye una variable, su trabajo se hace aún más fácil.
Al resolver para X en una ecuación polinómica, si se olvida de factorizar el GCF, es posible que se pierda una solución, y que podría mezclar que en más de un sentido! Sin esa solución, que podría terminar con un gráfico incorrecto para su polinomio. Y entonces todo su trabajo sería para nada!
Para factorizar el polinomio 6X4 - 12X3 + 4X2, por ejemplo, siga estos pasos:
Divida cada término en factores primos.
Este paso se expande la expresión original para
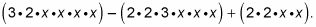
Puedes buscar los factores que aparecen en cada plazo para determinar el GCF.
En este ejemplo, se puede ver uno 2 y dos X's en cada término:
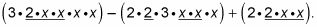
El GCF aquí es 2X2.
Factor del GCF hacia fuera de todo término delante de los paréntesis y el grupo de los restos dentro de los paréntesis.
Ahora tiene
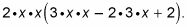
Multiplica cada término para simplificar.
La forma simplificada de la expresión que se encuentra en el paso 3 es 2X2(3X2 - 6X + 2).
Para ver si factorizado correctamente, distribuir el GCF y ver si obtiene el polinomio inicial. Si se multiplica el 2X2 dentro de los paréntesis, se obtiene 6X4 - 12X3 + 4X2. Ahora puede decir con confianza que 2X2 es el MCD.
Cómo factorizar las variables Usted puede factorizar las variables de los términos en una expresión. Se toma a cabo las variables de la misma manera como lo hace números excepto que cuando se toma fuera poderes de una variable, los más pequeño poder que aparece en un mismo…
Simplificar y factorizar expresiones En álgebra, la simplificación y factoring expresiones son procesos opuestos. Simplificar una expresión a menudo significa eliminación un par de parentheses- factorizar una expresión a menudo significa aplicar ellos.Supongamos que comienza con…
Completando el cuadrado para las secciones cónicas Cuando la ecuación de una sección cónica no está escrito en su forma estándar, completando el cuadrado es la única manera de convertir la ecuación a su forma estándar. Los pasos del proceso son los siguientes:Añadir / restar cualquier…
Factoring cuatro o más términos agrupando Cuando un polinomio tiene cuatro o más términos, la forma más fácil de factorizar que es usar agrupación. En este método, nos fijamos en sólo dos términos a la vez para ver si cualquiera de las técnicas se hacen evidentes. Por ejemplo,…
Encontrar las raíces de una ecuación factorizada En pre-cálculo, puede utilizar la propiedad del producto cero a encontrar las raíces de una ecuación factorizada. Después se toma un polinomio en sus diferentes piezas, puede configurar cada pieza igual a cero para resolver las raíces con la…
Cómo romper una diferencia cúbica o la suma Después de que se haya registrado para ver si hay un máximo común divisor (MCD) de un polinomio dado y descubrió que es un binomio que no es una diferencia de cuadrados, se debe considerar que puede ser una diferencia o suma de cubos.LA…
¿Cómo distinguir expresiones racionales propias e impropias Integración por fracciones parciales sólo funciona con expresiones racionales adecuadas, pero no con expresiones racionales impropias. Decirle a una fracción propia a partir de uno inadecuada es fácil: Una fracción a / b es correcta si el…
Cómo factorizar un cuadrado perfecto FOIL significa multiplicar la primero, afuera, adentro, y último términos juntos. Cuando una lámina de veces binomiales sí mismo, el producto se llama una cuadrado perfecto. Por ejemplo, (la + b)2 le da el trinomio cuadrado perfecto la2 + 2una B…
Cómo factorizar expresiones matemáticas A menudo se necesita factor expresiones (rompen esas expresiones en sus componentes más simples, o factores) Para el cálculo. Medios de factoring " unmultiplying, " como la reescritura de 12 comoNo encuentras con problemas como que en el cálculo,…
Cómo factorizar una expresión polinómica En matemáticas, factorización o factorización es la ruptura aparte de un polinomio en un producto de polinomios otros más pequeños. Si lo desea, usted podría entonces multiplicar estos factores juntos, y usted debe obtener el polinomio…
¿Cómo encontrar las raíces reales de un polinomio utilizando la regla de los signos de Descartes Si sabe el número de raíces totales un polinomio tiene, puede utilizar un teorema muy bien llamada Regla de los signos de Descartes a contar cuántas raíces son números reales (tanto positivos y negativa) y cuántos son imaginarios. Usted ve, el…
¿Cómo adivinar y comprobar raíces reales - 1 - lista de todas las posibles raíces racionales Cuando usted busca todo lo posible raíces racionales de cualquier polinomio, el primer paso es utilizar el teorema de la raíz racional para mencionarlos a todos.El teorema de la raíz racional dice que si usted toma todos los factores de la…