¿Cómo encontrar el límite de una función algebraica
Cuando su profesor de pre-cálculo le pide que encontrar el límite de una función algebraica, usted tiene cuatro técnicas para elegir: enchufar el X
Conteúdo
El mejor lugar para comenzar es la primera técnica. Sólo puede utilizar esta técnica si la función es continua en la X valor en el que usted está tomando el límite. Si la función no está definida en este X valor, se debe pasar a las otras técnicas para simplificar su función de manera que se puede conectar en el valor acercado para X.
Encontrar el límite enchufando el X valor
La primera técnica para resolver algebraicamente para un límite es para tapar el número que X Se acerca a la función. Si obtiene un valor indefinido (0 en el denominador), debe pasar a otra técnica. Pero si su función es continua en ese X valor, se obtendrá un valor, y ya está hecho- que ha encontrado su límite! Por ejemplo, con este método se puede encontrar este límite:
El límite es 3, porque F(5) = 3 y esta función es continua en X = 5.
Encontrar el límite de factoring
El factoraje es el método para tratar al enchufar falla - especialmente cuando cualquier parte de la función dada es una expresión polinómica.
Di que lo pedirá para encontrar este límite:
Usted primero intenta conectar 4 en la función, y se obtiene 0 en el numerador y el denominador, que le dice al pasar a la siguiente técnica. La expresión cuadrática en el numerador grita para que usted intente factoring ella. Observe que el numerador de los factores función anterior a (X - 4) (X - 2). los X - 4 se cancela en la parte superior y la parte inferior de la fracción. Este paso le deja con F(X) = X - 2. Puede conectar 4 a esta función continua para conseguir 2.
Si graficas esta función, parece que la línea recta F(X) = X - 2, pero tiene un agujero cuando X = 4 porque la función original sigue siendo indefinido allí (porque crea 0 en el denominador). La figura ilustra esto.
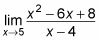
Si, después de haber considerado la parte superior e inferior de la fracción, un término en el denominador no canceló y el valor que usted está buscando no está definido, el límite de la función en que el valor de X no existe (que se puede escribir como DNE).
Por ejemplo, estos factores de función, como se muestra:
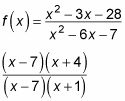
Los (X - 7) en la parte superior e inferior se anulan. Así que si se le pide que encontrar el límite de la función como X enfoques 7, se puede conectar 7 en la versión cancelada y obtener 8.11. Pero si usted está tratando de encontrar
la DNE límite, porque se ponía 0 en el denominador. Esta función, por lo tanto, tiene un límite en cualquier lugar excepto como X enfoques -1.
Encontrar el límite racionalizando el numerador
La tercera técnica que necesita saber para encontrar límites algebraicamente requiere para racionalizar el numerador. Funciones que requieren este método tienen una raíz cuadrada en el numerador y una expresión polinómica en el denominador. Por ejemplo, digamos que usted le pide que encontrar el límite de esta función como X enfoques 13:
La conexión de los números falla cuando llegues 0 en el denominador de la fracción. Factoring falla porque la ecuación no tiene polinomio al factor. En esta situación, si se multiplica el numerador y el denominador por el conjugado del numerador, el término en el denominador de que era un problema anula, y usted será capaz de encontrar el límite:
Multiplicar la parte superior e inferior de la fracción por el conjugado.
El conjugado del numerador es
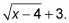
Multiplicando por medio, se obtiene esta configuración:
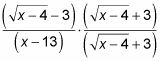
Frustrar el numerador para obtener
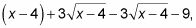
lo que simplifica a X - 13 (los dos términos medios cancelar y que combinan términos semejantes del FOIL).
Cancelar factores.
Cancelación le da esta expresión:
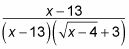
Los (X - 13) Los términos se anulan, dejando con este resultado:
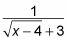
Calcular los límites.
Al conectar 13 en la función, se obtiene un sexto, que es el límite.
Encontrar el límite por encontrar el mínimo común denominador
Cuando te dan una función racional compleja, se utiliza la cuarta y última técnica límite de investigación algebraica. La técnica de taponamiento falla, porque usted termina con un 0 en uno de los denominadores. La función no es factorizable, y no tiene raíces cuadradas para racionalizar. Por lo tanto, usted sabe para pasar a la última técnica. Con este método, se combinan las funciones por encontrar el mínimo común denominador (LCD). Los términos se anulan, momento en el que se puede encontrar el límite.
Por ejemplo, siga los pasos para encontrar el límite:
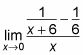
Encuentra la pantalla LCD de las fracciones en la parte superior.
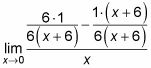
Distribuir los numeradores en la parte superior.
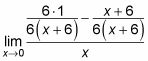
Sumar o restar los numeradores y luego cancelar términos.
Restando los numeradores le da
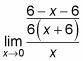
que luego se reduce a
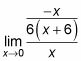
Utilice las reglas de fracciones para simplificar aún más.
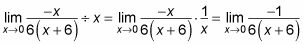
Sustituya el valor límite en esta función y simplificar.
Usted quiere encontrar el límite, cuando X enfoques 0, por lo que el límite aquí es -1/36.
¿Cómo distinguir expresiones racionales propias e impropias Integración por fracciones parciales sólo funciona con expresiones racionales adecuadas, pero no con expresiones racionales impropias. Decirle a una fracción propia a partir de uno inadecuada es fácil: Una fracción a / b es correcta si el…
Cómo calcular el límite de una función analítica Si tu profesor de pre-cálculo le pide para estimar el límite de una función analítica, puede simplemente crear un gráfico y poner el número que X es acercarse justo en el medio de ella. Luego, desde la izquierda en la misma fila, elija…
¿Cómo encontrar el límite de una función gráfica Cuando se te da la gráfica de una función y su profesor de pre-cálculo le pide que encontrar el límite, usted lee los valores de la gráfica - algo que has estado haciendo desde que usted aprendió lo que era un gráfico! Si usted está buscando…
Cómo racionalizar un radical de un denominador Una convención de las matemáticas es que usted no deja radicales en el denominador de una expresión cuando se escribe en su forma final. Así que hacemos algo que se llama racionalizar el denominador. Esta convención hace que la recogida como…
¿Cómo resolver un problema de límite de plug-and-chu Algunos problemas de límite, como los problemas de plug-and-chug, son muy fáciles de resolver. Sólo tiene que conectar el número de flecha en la función de límite, y si los resultados de cálculo de un número, esa es su respuesta (pero ver la…
¿Cómo resolver los límites de factoring Usted puede utilizar la técnica algebraica de factoring para resolver " verdadero " problemas de límite. Todos los métodos algebraicos implican la misma idea básica. Cuando la sustitución no funciona en la función original - por lo general a…
¿Cómo resolver los límites de la multiplicación conjugada Para resolver ciertos problemas de límite, tendrá la técnica de multiplicación conjugado. Cuando la sustitución no funciona en la función original - por lo general a causa de un agujero en la función - se puede usar la multiplicación…
¿Cómo resolver los límites en el infinito mediante el uso de asíntotas horizontales Asíntotas horizontales y límites en el infinito siempre van de la mano. No se puede tener uno sin el otro. Si usted tiene una función racional comodeterminar el límite en el infinito o infinito negativo es lo mismo que encontrar la ubicación de…
¿Cómo resolver límites con álgebra básica Cuando la sustitución no funciona en la función de límite inicial - por lo general a causa de un agujero en la función - a menudo se puede usar un poco de álgebra para manipular la función hasta la sustitución funciona (funciona porque su…
Cómo utilizar l'h & # regla del 244-pital para resolver problemas de límite Regla de L'H # de 244-pital es un gran atajo para hacer algunos problemas de límite. (Y es posible que se necesite algún día para resolver algunos problemas integrales impropias, y también para algunos problemas de series infinitas.)Al igual que…
Límites y continuidad en pre-cálculo En matemáticas, una límite sugiere que usted está acercando a un cierto valor. Algunas funciones, tales como una función racional con una asíntota horizontal, tienen un límite como el X los valores se mueven hacia el infinito positivo o…
¿Cómo encontrar identidades medio-ángulo para tangente La media de ángulo trig identidad para tangente tiene dos versiones. En lugar de que esto sea una molestia, que tiene más de una opción es realmente bastante agradable, porque se puede elegir la versión que mejor se adapte a su situación. Las…