Cómo utilizar l'h & # regla del 244-pital para resolver problemas de límite
Regla de L'H # de 244-pital es un gran atajo para hacer algunos problemas de límite. (Y es posible que se necesite algún día para resolver algunos problemas integrales impropias, y también para algunos problemas de series infinitas.)
Al igual que con la mayoría de los problemas de límites - sin contar obviedad problemas - no se puede hacer
con sustitución directa: 3 en enchufar X le da 0/0, que no está definido. La forma algebraica de hacer el límite es factorizar el numerador en (X - 3) (X + 3) y luego cancelar la (X - 3). Eso te deja con
que es igual a 6.
Ahora ver lo fácil que es tomar el límite con la regla de L'H # de 244-pital. Basta con tomar la derivada del numerador y el denominador. No utilice el cociente REGLA simplemente tomar los derivados del numerador y el denominador por separado. La derivada de X2 - 9 es 2X y el derivado de X - 3 es la regla 1. L'H # de 244-pital le permite reemplazar el numerador y el denominador por sus respectivos derivados como éste:
El nuevo límite es una obviedad:
Eso es todo al respecto. L'H regla # de 244-pital transforma un límite que no se puede ver con la sustitución directa en uno que puede hacer con la sustitución. Eso es lo que hace que sea un gran atajo tales.
Aquí está el galimatías matemático.
Regla de L'H # de 244-pital: Dejar F y g ser funciones diferenciables.
Sustitución le da 0/0 de modo se aplica la regla de L'H # de 244-pital.
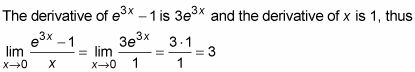
Tenga en cuenta que para utilizar la regla de L'H # de 244-pital, la sustitución debe producir cualquiera
Usted debe conseguir uno de estos aceptable " indeterminada " formas con el fin de aplicar el método abreviado. No se olvide de comprobar esto.
Cómo determinar los límites de secuencias con l'h & # 244-pital gobierno de Usted puede utilizar la regla de L'H # de 244-pital de encontrar límites de sucesiones. Regla de L'H # de 244-pital es un gran atajo para cuando haces limitar problemas. Aquí está:Convergencia y Divergencia: Usted dice que una secuencia converge…
¿Cómo encontrar primitivas con el método de sustitución Cuando el argumento de una función (que es la entrada de la función) es más complicado que algo así como 3X + 2 (a lineal funcion de X - es decir, una función donde X se eleva a la primera potencia), puede utilizar el método de sustitución.…
¿Cómo encontrar derivados utilizando las normas de productos y cocientes Hay reglas especiales para encontrar la derivada del producto de dos funciones o el cociente de dos funciones- estos son la regla del producto y de la regla del cociente, respectivamente.Estado del producto: Se utiliza la regla del producto para -…
¿Cómo encontrar el límite de una función algebraica Cuando su profesor de pre-cálculo le pide que encontrar el límite de una función algebraica, usted tiene cuatro técnicas para elegir: enchufar el X valor, el factoring, racionalizar el numerador, y encontrar el mínimo común denominador.El…
¿Cómo integrar expresiones racionales utilizando la suma, constante múltiple, y las reglas de alimentación En muchos casos, puede desenredar expresiones racionales peludas e integrarlos utilizando las reglas anti-diferenciación más la regla de la suma, la Regla múltiplo constante, y la Regla de energía.La regla de la suma para la integración le dice…
Cómo hacer inaceptables formas aceptables antes de usar l'h & # regla del 244-pital Usted puede utilizar la regla de L'H # de 244-pital de encontrar un límite cuando otros métodos no funcionan. De hecho, incluso si algún otro método funciona, regla de L'H # de 244-pital es a menudo un buen atajo. Si la sustitución del número…
¿Cómo resolver integrales con la sustitución de variables En cálculo, puede utilizar la sustitución de variables para evaluar una integral compleja. Sustitución de variables permite integrar cuando la regla de la suma, la Regla múltiplo constante, y la Regla de energía no funcionan.Declare una…
¿Cómo resolver los límites de factoring Usted puede utilizar la técnica algebraica de factoring para resolver " verdadero " problemas de límite. Todos los métodos algebraicos implican la misma idea básica. Cuando la sustitución no funciona en la función original - por lo general a…
¿Cómo resolver los límites de la multiplicación conjugada Para resolver ciertos problemas de límite, tendrá la técnica de multiplicación conjugado. Cuando la sustitución no funciona en la función original - por lo general a causa de un agujero en la función - se puede usar la multiplicación…
¿Cómo resolver los límites en el infinito mediante el uso de asíntotas horizontales Asíntotas horizontales y límites en el infinito siempre van de la mano. No se puede tener uno sin el otro. Si usted tiene una función racional comodeterminar el límite en el infinito o infinito negativo es lo mismo que encontrar la ubicación de…
¿Cómo resolver límites con álgebra básica Cuando la sustitución no funciona en la función de límite inicial - por lo general a causa de un agujero en la función - a menudo se puede usar un poco de álgebra para manipular la función hasta la sustitución funciona (funciona porque su…
¿Cómo transformar los problemas de límites con el fin de utilizar l'h & # regla del 244-pital Aunque la regla de L'H # de 244-pital es un gran atajo para hacer problemas de límite, puede ser a veces no puede continuar con un problema de límite cuando la sustitución produce formas inaceptables,En estos casos, primero hay que ajustar el…