¿Cómo integrar expresiones racionales utilizando la suma, constante múltiple, y las reglas de alimentación
En muchos casos, puede desenredar expresiones racionales peludas e integrarlos utilizando las reglas anti-diferenciación más la regla de la suma, la Regla múltiplo constante, y la Regla de energía.
La regla de la suma para la integración le dice que la integración de expresiones largas término a término está bien. Sentimos formalmente:
La Regla múltiple Constante le dice que usted puede mover un fuera constante de un derivado antes de integrar. Aquí se expresa en símbolos:
La regla de la potencia para la integración le permite integrar cualquier poder real de X (excepto -1). Aquí está la regla de la potencia expresado formalmente:
Aquí hay un integrante que parece que puede ser difícil:
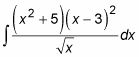
Se puede dividir la función en varias fracciones, pero sin la regla del producto o regla del cociente, estás entonces atascado. En su lugar, ampliar el numerador y el denominador poner en forma exponencial:
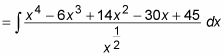
A continuación, dividir la expresión en cinco términos:
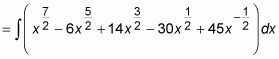
A continuación, utilice la regla de la suma para separar la integral en cinco integrales separadas y la Regla múltiplo constante para mover el coeficiente de fuera de la integral en cada caso:
Ahora usted puede integrar cada término por separado utilizando la regla de la potencia:
-
Reglas de cálculo básicas para la economía de la empresa -
Aplicando orden de operaciones para expresiones con solamente la suma y resta -
Cálculo II para dummies -
Encontrar la integral de un producto de dos funciones -
Encuentra la integral de funciones anidadas -
Cómo antidifferentiate cualquier polinomio utilizando la suma, constante múltiple, y las reglas de alimentación
Cómo aproximar área con la regla de Simpson Con la regla de Simpson, que aproximar el área bajo una curva con curvas-coronado " trapezoides ". La parte superior de estas formas son secciones de parábolas. Usted puede llamar " trapezoides " porque juegan el mismo papel en la regla de Simpson…
¿Cómo encontrar primitivas utilizando reglas inversas Puede utilizar las reglas inversas para encontrar primitivas. Las más sencillas reglas antiderivada son los que son lo contrario de las normas derivadas que ya conoce. Estos son, primitivas automáticos de un solo paso con la excepción de la regla…
¿Cómo encontrar derivados utilizando las normas de productos y cocientes Hay reglas especiales para encontrar la derivada del producto de dos funciones o el cociente de dos funciones- estos son la regla del producto y de la regla del cociente, respectivamente.Estado del producto: Se utiliza la regla del producto para -…
¿Cómo integrar una serie de potencias Debido a la serie de potencia se asemejan polinomios, son fáciles de integrar el uso de un proceso de tres pasos simples que utiliza la regla de la suma, la Regla múltiplo constante, y la Regla de energía.Por ejemplo, echar un vistazo a la…
¿Cómo integrar una función multiplicada por un conjunto de funciones anidadas A veces es necesario integrar el producto de una función (X) Y una composición de funciones (por ejemplo, la función 3X2 + 7 anidada dentro de una función de raíz cuadrada). Si estaba diferenciando, podría utilizar una combinación de la regla…
¿Cómo integrar potencias impares de senos y cosenos Puede integrar alguna función de la forma pecadom X cosn X cuando m es impar, para cualquier valor real de n. Para este procedimiento, tenga en cuenta el pecado identidad trigonométrica útil2 X + cos2 X = 1. Por ejemplo, aquí es cómo…
¿Cómo integrar potencias pares de senos y cosenos Puede integrar poderes incluso de senos y cosenos. Por ejemplo, si desea integrar el pecado2 X y cos2 X, que utilizaría estas identidades trigonométricas dos semi-ángulo:He aquí cómo usted integra cos2 X:Utilice la identidad-medio ángulo para…
¿Cómo resolver integrales con la sustitución de variables En cálculo, puede utilizar la sustitución de variables para evaluar una integral compleja. Sustitución de variables permite integrar cuando la regla de la suma, la Regla múltiplo constante, y la Regla de energía no funcionan.Declare una…
La integración usando fracciones parciales cuando el denominador contiene factores irreducibles cuadráticas Usted puede utilizar el método de fracciones parciales para integrar las funciones racionales, incluyendo funciones con denominadores que contienen irreducible factores de segundo grado (es decir, los factores de segundo grado que no puede…
Saber cuándo integrar por partes Es importante reconocer que la integración por partes es útil. Para empezar, aquí hay dos casos importantes cuando la integración por partes es definitivamente el camino a seguir:La función logarítmica ln XLas cuatro primeras funciones…
La creación de fracciones parciales cuando se tiene factores lineales distintos Su primer paso en cualquier problema que involucra fracciones parciales es reconocer cuyo caso usted está tratando con lo que pueda solucionar el problema. El caso más simple en el que las fracciones parciales son útiles es cuando el denominador…
Sustituyendo con expresiones de la forma f (x) multiplicado por g (x) Cuando g'(X) = F(X), Puede utilizar la sustitución u = g(X) Para integrar expresiones de la forma F(X) multiplicada por g(X). Sustitución de variables ayuda a llenar el vacío dejado por la ausencia de una regla del producto y una regla de la…