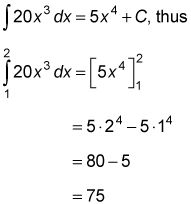¿Cómo encontrar primitivas utilizando reglas inversas
Puede utilizar las reglas inversas para encontrar primitivas. Las más sencillas reglas antiderivada son los que son lo contrario de las normas derivadas que ya conoce. Estos son, primitivas automáticos de un solo paso con la excepción de la regla de la potencia inversa, que es sólo un poco más difícil.
Usted sabe que la derivada del pecado X es cos X, así que de marcha atrás que te dice que una antiderivada de cos X es pecado X. ¿Qué podría ser más simple? Pero no se olvide que todas las funciones de la forma pecado X + C son primitivas de cos X. En símbolos, escribes
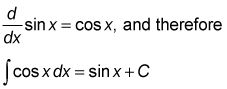
Esta tabla muestra las reglas inversas para primitivas.
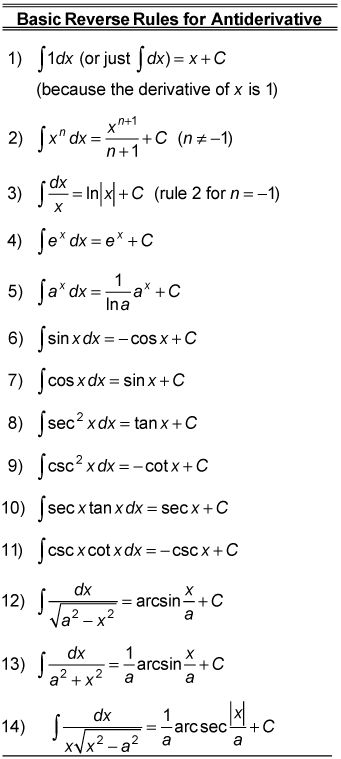
También puede utilizar el (un poco más difícil) regla de la potencia inversa. Por la regla de la potencia para la diferenciación, ya lo sabes
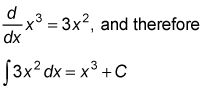
Aquí está el método simple para la inversión de la regla de la potencia. Usar y - 5X4 para su función. Recordemos que la regla de la potencia dice
Lleve el poder frente a donde quiere multiplicar el resto del derivado.
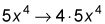
Reducir el poder de uno y simplificar.
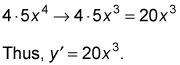
Para revertir este proceso, se invierte el orden de los dos pasos y revertir las matemáticas dentro de cada paso. He aquí cómo funciona para el problema anterior:
Aumentar el poder por una.
El 3 se convierte en un 4.
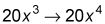
Dividir por el nuevo poder y simplificar.
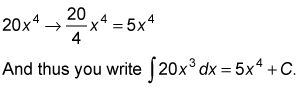
Por supuesto, todas las mejores reglas contienen algún tipo de advertencia, y esto no es una excepción.
La regla de la potencia inversa no funciona para un poder de uno negativo. La regla de la potencia inversa funciona para todos los poderes (incluyendo poderes negativos y decimales) a excepción de un poder de uno negativo. En lugar de utilizar la regla de potencia inversa, sólo debe memorizar que la antiderivada de
(regla de las 3 de la tabla).
Pon a prueba tus primitivas diferenciando ellos. Especialmente cuando eres nuevo en antidiferenciación, es una buena idea para poner a prueba sus primitivas diferenciando ellos - se puede pasar por alto el C. Si usted consigue de nuevo a su función original, usted sabe que su primitiva es la correcta.
Con la antiderivada usted acaba de encontrar y utilizar el teorema fundamental, se puede determinar el área bajo 20X3 entre, por ejemplo, 1 y 2:
Cálculo: cómo resolver los problemas de diferenciación En cálculo, la forma de resolver un problema derivado depende de qué forma el problema toma. Tipos de problemas comunes incluyen la cadena REGLA posición Optimization, la velocidad y las tasas acceleration- y relacionados. Aquí están algunas…
Cómo coeficientes afectan a la diferenciación Si la función que está diferenciando comienza con un coeficiente, el coeficiente no tiene efecto sobre el proceso de diferenciación. Usted sólo lo ignora y se diferencian de acuerdo a la norma correspondiente. El coeficiente se queda donde…
Cómo antidifferentiate cualquier polinomio utilizando la suma, constante múltiple, y las reglas de alimentación Las reglas anti-diferenciación para la integración en gran medida limitar el número de integrales se puede calcular fácilmente. En muchos casos, sin embargo, puede integrar alguna polinomio en tres pasos utilizando la regla de la suma, la Regla…
¿Cómo diferenciar funciones inversas Hay una fórmula difícil buscar la participación de las derivadas de las funciones inversas, pero antes de llegar a eso, a ver la figura siguiente, que resume muy bien la idea.Esta cifra muestra un par de funciones inversas, F y g. Funciones…
¿Cómo diferenciar implícitamente A veces se le pide para diferenciar una ecuación que no está resuelto por y, como y5 + 3X2 = Sen X - 4y3. Esta ecuación define y de forma implícita como una función de X, y no se puede escribir como una función explícita porque no puede ser…
¿Cómo encontrar primitivas por adivinar y comprobar El método de estimación y comprobación funciona cuando el integrando - eso es lo que deseas antidifferentiate (la expresión después del símbolo integral, sin contar el dx) - Está cerca de una función que ya sabes la regla inversa para. Por…
¿Cómo encontrar primitivas con el método de sustitución Cuando el argumento de una función (que es la entrada de la función) es más complicado que algo así como 3X + 2 (a lineal funcion de X - es decir, una función donde X se eleva a la primera potencia), puede utilizar el método de sustitución.…
¿Cómo encontrar derivados utilizando las normas de productos y cocientes Hay reglas especiales para encontrar la derivada del producto de dos funciones o el cociente de dos funciones- estos son la regla del producto y de la regla del cociente, respectivamente.Estado del producto: Se utiliza la regla del producto para -…
¿Cómo integrar potencias impares de senos y cosenos Puede integrar alguna función de la forma pecadom X cosn X cuando m es impar, para cualquier valor real de n. Para este procedimiento, tenga en cuenta el pecado identidad trigonométrica útil2 X + cos2 X = 1. Por ejemplo, aquí es cómo…
¿Cómo integrar expresiones racionales utilizando la suma, constante múltiple, y las reglas de alimentación En muchos casos, puede desenredar expresiones racionales peludas e integrarlos utilizando las reglas anti-diferenciación más la regla de la suma, la Regla múltiplo constante, y la Regla de energía.La regla de la suma para la integración le dice…
Cómo utilizar la regla de la cadena para encontrar la derivada de funciones anidadas A veces, cuando lo que necesita para encontrar la derivada de una función anidada con la regla de la cadena, averiguar qué función está dentro de lo que puede ser un poco difícil - especialmente cuando una función está anidado dentro de otro…
Las reglas básicas de diferenciación Algunas reglas de diferenciación son muy fácil de recordar y utilizar. Estos incluyen la regla constante, regla de la potencia, la regla múltiplo constante, regla de suma, y la regla diferencia.La regla constante: Este es simple. F (X) = 5…