¿Cómo integrar potencias impares de senos y cosenos
Puede integrar alguna función de la forma pecadom X cosn X cuando m es impar, para cualquier valor real de n. Para este procedimiento, tenga en cuenta el pecado identidad trigonométrica útil2 X + cos2 X = 1. Por ejemplo, aquí es cómo integrar
Despegar un pecado X y colocarlo junto a la dx:
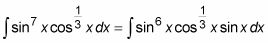
Aplique el pecado identidad trigonométrica2 X = 1 - cos2 X para expresar el resto de los senos en la función como cosenos:
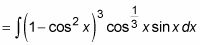
Utilice la sustitución de variables u = Cos X y du = -sen x dx:
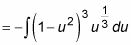
Ahora que tiene la función en términos de poderes de u, lo peor ha pasado. Puede ampliar la función de salida, convirtiéndolo en un polinomio. Esto es sólo el álgebra:
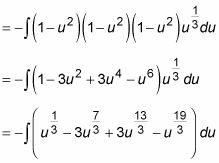
Para continuar, utilice la regla de la suma y la Regla múltiplo constante de separar esto en cuatro integrales. No te olvides de distribuir ese signo menos a las cuatro integrales!
En este punto, se puede evaluar cada integrante separado utilizando la regla de la potencia:
Por último, utilice u = Cos X para revertir la sustitución de variables:
Observe que cuando sustituyes atrás en términos de X, se va al lado de las cos en lugar de al lado de la X, porque usted está levantando toda la función cos X a una potencia.
Del mismo modo, a integrar alguna función de la forma pecadom X cosn X cuando n es impar, para cualquier valor real de m. Estos pasos son prácticamente los mismos que en el ejemplo anterior. Por ejemplo, aquí es cómo integrar el pecado-4 X cos9 X:
Despegar a cos X y colocarlo junto a la dx:
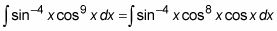
Aplicar las cos identidad trigonométrica2 X = 1 - sen2 X para expresar el resto de los cosenos en la función como senos:
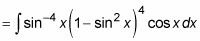
Utilice la sustitución de variables u = Sen X y du = Cos x dx:
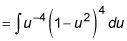
En este punto, puede distribuir la función y expresarlo como una suma de potencias de u.
-
Cálculo II para dummies -
Expresando la función sen x como una serie -
Encontrar la integral de un producto de dos funciones -
Cómo antidifferentiate cualquier polinomio utilizando la suma, constante múltiple, y las reglas de alimentación -
¿Cómo integrar una serie de potencias -
¿Cómo integrar potencias pares de secantes con tangentes
¿Cómo integrar potencias impares de tangentes con secantes Puede integrar potencias impares de tangentes con secantes. Integrar bronceadom X segundon X cuando m es extraño - por ejemplo, bronceado7 X segundo9 X - usted sigue estos pasos:Despegar un bronceado X y un segundo X y colocarlos al lado del…
¿Cómo integrar los problemas de seno / coseno con una potencia extraña, positivo de seno He aquí cómo usted integra un integrante trig que contiene senos y cosenos, donde el poder de seno es impar y positivo. Usted cortar un factor sine y ponerlo a la derecha del resto de la expresión, convertir los restantes (incluso) factores seno…
¿Cómo integrar expresiones racionales utilizando la suma, constante múltiple, y las reglas de alimentación En muchos casos, puede desenredar expresiones racionales peludas e integrarlos utilizando las reglas anti-diferenciación más la regla de la suma, la Regla múltiplo constante, y la Regla de energía.La regla de la suma para la integración le dice…
¿Cómo integrar potencias pares de senos y cosenos Puede integrar poderes incluso de senos y cosenos. Por ejemplo, si desea integrar el pecado2 X y cos2 X, que utilizaría estas identidades trigonométricas dos semi-ángulo:He aquí cómo usted integra cos2 X:Utilice la identidad-medio ángulo para…
¿Cómo integrar los problemas de seno / coseno con una potencia extraña, positivo de coseno Mediante la integración de un integrante trig que incluye coseno, y si el poder del coseno es impar y positivo, puede convertir y luego utilizar la sustitución de integrar. Para hacer esta conversión, lo que necesita saber la identidad de…
¿Cómo simplificar una expresión utilizando par / impar identidades Debido seno, coseno, y la tangente son funciones (funciones trigonométricas), que pueden definirse como pares o impares funciones. Sine y la tangente son funciones impares, y el coseno es una función par. En otras palabras,pecado(-X) = -sen Xcos…
¿Cómo resolver integrales con la sustitución de variables En cálculo, puede utilizar la sustitución de variables para evaluar una integral compleja. Sustitución de variables permite integrar cuando la regla de la suma, la Regla múltiplo constante, y la Regla de energía no funcionan.Declare una…
Cómo utilizar identidades para integrar las funciones trigonométricas Usted se sorprenderá de lo mucho que avanzar a menudo se puede hacer cuando se integra una función de trigonometría desconocida por primera ajustar usando las identidades Básica Cinco trig:El poder invisible de estas identidades se encuentra en…
Integrar, cuando los poderes de seno, coseno son aún, no negativo Cuando los poderes tanto de seno y coseno son uniformes y no negativo, se puede convertir el integrando en potencias impares de cosenos mediante el uso de las siguientes identidades trigonométricas.Dos identidades trigonométricas prácticos:Luego…
Integrar una función utilizando el caso sine Cuando la función está integrando incluye un término de la forma (la2 - bx2)n, llamar su triángulo sustitución trigonométrica para el caso sinusoidal. Por ejemplo, supongamos que desea evaluar la siguiente integral:Este es un caso sinusoidal,…
La integración de los poderes de cotangentes y cosecantes Puede integrar poderes de cotangentes y cosecantes similares a la forma de hacer las tangentes y secantes. Por ejemplo, aquí es cómo integrar cuna8 X csc6 X:Despegar un csc2 X y colocarlo junto a la dx:Utilice la identidad trigonométrica 1 +…
Saber cuándo integrar por partes Es importante reconocer que la integración por partes es útil. Para empezar, aquí hay dos casos importantes cuando la integración por partes es definitivamente el camino a seguir:La función logarítmica ln XLas cuatro primeras funciones…