Integrar, cuando los poderes de seno, coseno son aún, no negativo
Cuando los poderes tanto de seno y coseno son uniformes y no negativo, se puede convertir el integrando en potencias impares de cosenos mediante el uso de las siguientes identidades trigonométricas.
Dos identidades trigonométricas prácticos:

Luego de terminar el problema mediante la conversión de los cosenos restantes para senos con la identidad de Pitágoras, simplificando, y luego la integración con la sustitución. He aquí un ejemplo:
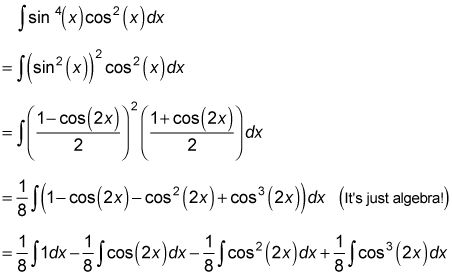
El primero de esta cadena de integrales es un no-brainer- el segundo es una regla inversa simple con un pequeño arreglo para el 2- haces el tercer integrante utilizando el cos2 (X) La identidad de un segundo tiempo y manejar el cuarto integrante como lo hace cuando el poder del coseno es impar y positivo. Su respuesta final debe ser
Una caminata de la torta verdadera.
Don'olvide sus identidades trigonométricas. Si obtiene un problema en el que los poderes del seno y el coseno no son tanto uniforme y no negativo, trate de usar una identidad trigonométrica como
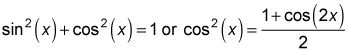
para convertir la integral en uno que puede manejar.
Por ejemplo, en
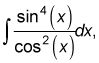
puede utilizar la identidad de Pitágoras para convertirlo en
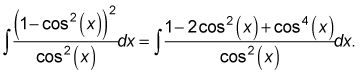
Este se divide en
y el resto es fácil. Intentalo. Vea si puede diferenciar su resultado y llegar de nuevo al problema original.






