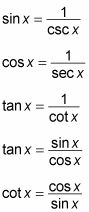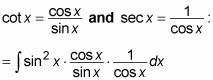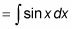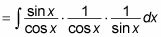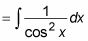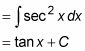Cómo utilizar identidades para integrar las funciones trigonométricas
Usted se sorprenderá de lo mucho que avanzar a menudo se puede hacer cuando se integra una función de trigonometría desconocida por primera ajustar usando las identidades Básica Cinco trig:
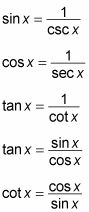
El poder invisible de estas identidades se encuentra en el hecho de que permiten que usted se exprese alguna combinación de trig funciones en una combinación de senos y cosenos. En términos generales, el truco consiste en simplificar una función trigonométrica poco familiar y convertirlo en algo que usted sabe cómo integrar.
Cuando te enfrentas a un producto desconocido o cociente de funciones trigonométricas, siga estos pasos:
Utilice identidades trigonométricas para convertir todos los factores en senos y cosenos.
Cancelar factores siempre que sea posible.
Si es necesario, utilizar identidades trigonométricas para eliminar todas las fracciones.
Por ejemplo:
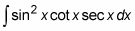
En su forma actual, no se puede integrar esta expresión. Así que sigue estos pasos para convertirlo en una expresión puede integrar:
Utilice las identidades
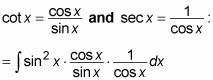
Cancelar tanto pecado X y cos X en el numerador y el denominador:
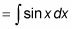
En este ejemplo, incluso sin la Etapa 3, que tiene una función que puede integrar.
= -cos X + C
He aquí otro ejemplo:
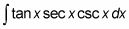
Una vez más, esta integral se parece a un callejón sin salida antes de aplicar los cinco identidades trigonométricas básicas a la misma:
Gire los tres factores en senos y cosenos:
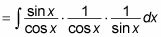
Cancelar el pecado X en el numerador y el denominador:
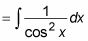
Utilice el cos de identidad X = 1 / sec X para eliminar la fracción:
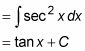
Esto activa una función desconocida en una función trigonométrica que usted sabe cómo integrar.
-
Más allá de lo básico con identidades trigonométricas -
Incluso identidades y pico en las funciones trigonométricas -
Primeros pasos con identidades trigonométricas -
¿Cómo integrar potencias impares de senos y cosenos -
¿Cómo integrar potencias pares de senos y cosenos -
¿Cómo demostrar una igualdad mediante el uso de identidades periodicidad
¿Cómo demostrar una igualdad usando identidades co-función Identidades Co-función pueden aparecer en trig pruebas. Si usted ve la expresión pi / 2 - X paréntesis dentro de cualquier función trigonométrica, es necesario utilizar una identidad co-función para la prueba. Siga los pasos para demostrar…
¿Cómo demostrar identidades trigonométricas cuando se suman o restan términos Cuando se añaden o restan los términos en una prueba trig, puede crear fracciones donde no estaban antes. Esto es especialmente cierto cuando se trata de la secante y cosecante, porque se crea fracciones cuando se convierte (respectivamente)…
¿Cómo demostrar identidades trigonométricas cuando usted comienza con fracciones Cuando la expresión trig te dan comienza con fracciones, la mayoría de las veces usted tiene que agregar (o restar) a conseguir cosas para simplificar. He aquí un ejemplo de una prueba donde hacer precisamente eso recupera el balón rodando.…
¿Cómo simplificar una expresión utilizando par / impar identidades Debido seno, coseno, y la tangente son funciones (funciones trigonométricas), que pueden definirse como pares o impares funciones. Sine y la tangente son funciones impares, y el coseno es una función par. En otras palabras,pecado(-X) = -sen Xcos…
¿Cómo simplificar una expresión utilizando identidades recíprocas Cuando se le pregunta para simplificar una expresión que implica cosecante, secante o cotangente, cambia la expresión de funciones que implican seno, coseno, tangente o, respectivamente. Al cambiar las funciones de esta manera, usted está…
¿Cómo simplificar una expresión utilizando identidades periodicidad Identidades Periodicidad ilustrar cómo trasladar la gráfica de una función trigonométrica por un período a los resultados de izquierda o derecha en la misma función. Las funciones de seno, coseno, secante, cosecante y repetir cada 2 (pi)…
Cómo simplificar expresiones trigonométricas con un binomio en el denominador de una fracción Cuando una expresión trigonométrica es una fracción con un binomio en su denominador, siempre tenga en cuenta multiplicando por el conjugado antes de hacer cualquier otra cosa. La mayoría de las veces, esta técnica permite simplificar.Por…
Integrar, cuando los poderes de seno, coseno son aún, no negativo Cuando los poderes tanto de seno y coseno son uniformes y no negativo, se puede convertir el integrando en potencias impares de cosenos mediante el uso de las siguientes identidades trigonométricas.Dos identidades trigonométricas prácticos:Luego…
La integración de los poderes de cotangentes y cosecantes Puede integrar poderes de cotangentes y cosecantes similares a la forma de hacer las tangentes y secantes. Por ejemplo, aquí es cómo integrar cuna8 X csc6 X:Despegar un csc2 X y colocarlo junto a la dx:Utilice la identidad trigonométrica 1 +…
Identidades pitagóricas básicos para funciones trigonométricas Las identidades pitagóricas son bloques de construcción para muchas de las manipulaciones de ecuaciones y expresiones trigonométricas. Proporcionan un mayor número de métodos para resolver problemas trigonométricos de manera más eficiente, ya…
Cambie de senos y cosenos en una identidad trigonometría Con algunas identidades trigonométricas, usted puede decidir para simplificar las cosas, ya sea cambiando todo para senos y cosenos o factoring a cabo alguna función. A veces, no está claro de qué lado usted debe trabajar en o lo que debe hacer…
Encuentra identidades relación trigonometría Trig tiene dos identidades llamados identidades de relación. Esta etiqueta puede ser confuso, ya que todas las funciones trigonométricas se definen por relaciones. En algún momento, sin embargo, los matemáticos pensaron que esta descripción era…