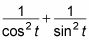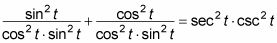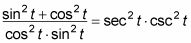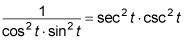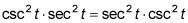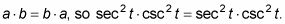¿Cómo demostrar identidades trigonométricas cuando se suman o restan términos
Cuando se añaden o restan los términos en una prueba trig, puede crear fracciones donde no estaban antes. Esto es especialmente cierto cuando se trata de la secante y cosecante, porque se crea fracciones cuando se convierte (respectivamente) para
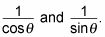
Lo mismo es cierto para la tangente cuando se cambia a
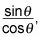
y cotangente convierte
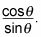
He aquí un ejemplo que ilustra este punto. Siga estos pasos para probar que
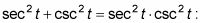
Convertir todas las funciones trigonométricas de senos y cosenos.
En la parte izquierda, ahora tiene
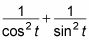
Encuentra el mínimo común denominador de las dos fracciones.
Esta multiplicación le da
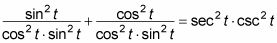
Añadir las dos fracciones.
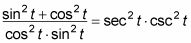
Simplifique la expresión de una identidad de Pitágoras en el numerador.
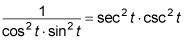
Utilice identidades recíprocas para invertir la fracción.
Ambas partes tienen ahora la multiplicación:
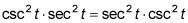
Tenga en cuenta que algunos maestros de pre-cálculo permiten dejar de allí- otros, sin embargo, te hacen volver a escribir la ecuación de modo que los lados izquierdo y derecho coinciden exactamente. Cada maestro tiene su propia manera de probar identidades trigonométricas. Asegúrese de que usted cumpla con expectativas, de lo contrario, puede perder puntos de su maestro en una prueba.
Utilice las propiedades de la igualdad de reescribir.
La propiedad conmutativa de la multiplicación dice que
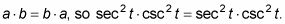
Sobre el autor
 ¿Cómo demostrar identidades complejas, trabajando los distintos lados de una prueba trig
¿Cómo demostrar identidades complejas, trabajando los distintos lados de una prueba trig A veces, haciendo el trabajo a ambos lados de una prueba trig, un lado a la vez, conduce a una solución más rápida. Esto se debe a que con el fin de demostrar una identidad muy complicado, es posible que necesite para complicar aún más la…
 ¿Cómo demostrar una igualdad usando identidades pitagóricas
¿Cómo demostrar una igualdad usando identidades pitagóricas Cuando se le preguntó para demostrar una identidad, si usted ve un negativo de una variable dentro de una función trigonométrica, se utiliza automáticamente un par / impar identidad. En primer lugar, sustituir todas las funciones…
 ¿Cómo demostrar identidades trigonométricas cuando usted comienza con fracciones
¿Cómo demostrar identidades trigonométricas cuando usted comienza con fracciones Cuando la expresión trig te dan comienza con fracciones, la mayoría de las veces usted tiene que agregar (o restar) a conseguir cosas para simplificar. He aquí un ejemplo de una prueba donde hacer precisamente eso recupera el balón rodando.…
 ¿Cómo simplificar una expresión utilizando par / impar identidades
¿Cómo simplificar una expresión utilizando par / impar identidades Debido seno, coseno, y la tangente son funciones (funciones trigonométricas), que pueden definirse como pares o impares funciones. Sine y la tangente son funciones impares, y el coseno es una función par. En otras palabras,pecado(-X) = -sen Xcos…
 ¿Cómo simplificar una expresión utilizando identidades recíprocas
¿Cómo simplificar una expresión utilizando identidades recíprocas Cuando se le pregunta para simplificar una expresión que implica cosecante, secante o cotangente, cambia la expresión de funciones que implican seno, coseno, tangente o, respectivamente. Al cambiar las funciones de esta manera, usted está…
 ¿Cómo simplificar una expresión utilizando identidades periodicidad
¿Cómo simplificar una expresión utilizando identidades periodicidad Identidades Periodicidad ilustrar cómo trasladar la gráfica de una función trigonométrica por un período a los resultados de izquierda o derecha en la misma función. Las funciones de seno, coseno, secante, cosecante y repetir cada 2 (pi)…
 Cómo utilizar identidades para integrar las funciones trigonométricas
Cómo utilizar identidades para integrar las funciones trigonométricas Usted se sorprenderá de lo mucho que avanzar a menudo se puede hacer cuando se integra una función de trigonometría desconocida por primera ajustar usando las identidades Básica Cinco trig:El poder invisible de estas identidades se encuentra en…
 Romper o combinar fracciones para resolver una identidad trigonometría
Romper o combinar fracciones para resolver una identidad trigonometría Una identidad trigonométrica con fracciones puede trabajar a su ventaja- te dan una plan de ataque. Usted puede trabajar hacia la eliminación de la fracción y, en el proceso, resolver el problema. Dos de las principales técnicas para trabajar…
 Cambie de senos y cosenos en una identidad trigonometría
Cambie de senos y cosenos en una identidad trigonometría Con algunas identidades trigonométricas, usted puede decidir para simplificar las cosas, ya sea cambiando todo para senos y cosenos o factoring a cabo alguna función. A veces, no está claro de qué lado usted debe trabajar en o lo que debe hacer…
 Sine Express en términos de secante o cosecante
Sine Express en términos de secante o cosecante A pesar de que cada función trigonométrica es perfectamente maravilloso, poder expresar cada función trig en términos de una de las otras cinco funciones trigonométricas es con frecuencia a su ventaja. Por ejemplo, usted puede tener algunos…
 Sine Express en términos de cotangente
Sine Express en términos de cotangente A pesar de que cada función de la trigonometría es perfectamente maravilloso, poder expresar cada función trig en términos de una de las otras cinco funciones trigonométricas es con frecuencia a su ventaja. Por ejemplo, usted puede tener…
 Encuentra identidades relación trigonometría
Encuentra identidades relación trigonometría Trig tiene dos identidades llamados identidades de relación. Esta etiqueta puede ser confuso, ya que todas las funciones trigonométricas se definen por relaciones. En algún momento, sin embargo, los matemáticos pensaron que esta descripción era…