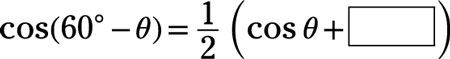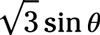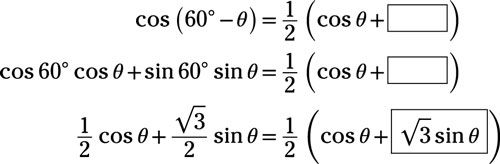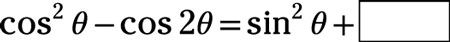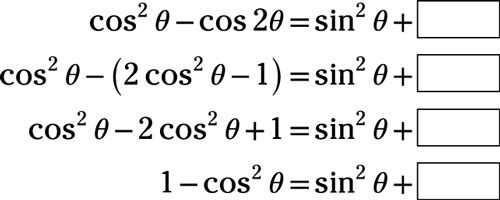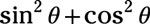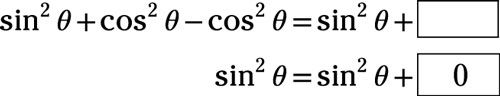Más allá de lo básico con identidades trigonométricas
Las identidades trigonométricas básicas se obtiene a través de la mayoría de los problemas y las aplicaciones relacionadas con la trigonometría. Pero si usted va a ampliar sus horizontes y estudiar más y más matemáticas, encontrará algunas identidades adicionales cruciales para su éxito. También, en algunas de las ciencias, especialmente la física, estas identidades especializadas surgen en los lugares más inverosímiles (y probables).
Estas identidades trigonométricas se dividen en grupos, dependiendo de si usted está tratando de combinar los ángulos o dividir aparte, aumentar exponentes o reducirlas, y así sucesivamente. Las agrupaciones pueden ayudar a decidir qué identidad a utilizar en cada situación. Mantenga una lista de estas identidades a mano, porque usted querrá referirse a ellos a medida que trabaja a través de los problemas.
Usted trabajará con las identidades trigonométricas más avanzadas de las siguientes maneras:
Usando los valores de la función de dos ángulos para determinar el valor de la función de la suma de los ángulos
La aplicación de las identidades de la diferencia entre dos ángulos
Haciendo uso de las identidades medio-ángulo
Trabajando a partir de identidades de producto a suma y suma a producto
El uso de los períodos de funciones en las identidades
La aplicación de las identidades de reducción de potencia
Decidir que la identidad de usar primero
Cuando usted está trabajando en estas identidades trigonométricas particulares, algunos desafíos incluirán lo siguiente:
Aplicando las identidades usando el orden correcto de las operaciones
La simplificación de los radicales correctamente en identidades medio ángulo
Tomar las decisiones correctas entre identidades positivas y negativas
Problemas de práctica
Utilice una identidad suma o diferencia para determinar el término que falta en la identidad:
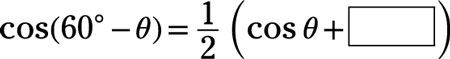
Responder:
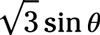
Utilice la identidad coseno-de-una diferencia:
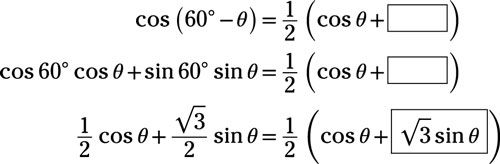
Utilice una identidad doble ángulo para determinar el término que falta en la identidad.
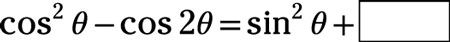
Responder: 0
Reemplazar

con la identidad de doble ángulo que implica el coseno:
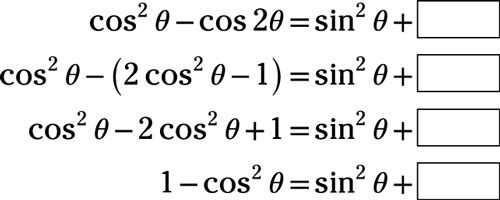
Vuelva a colocar el 1 con
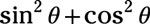
a partir de la identidad de Pitágoras:
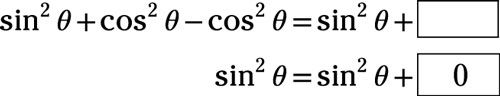
Sobre el autor
 Cómo utilizar identidades para integrar las funciones trigonométricas
Cómo utilizar identidades para integrar las funciones trigonométricas Usted se sorprenderá de lo mucho que avanzar a menudo se puede hacer cuando se integra una función de trigonometría desconocida por primera ajustar usando las identidades Básica Cinco trig:El poder invisible de estas identidades se encuentra en…
 Identidades pitagóricas básicos para funciones trigonométricas
Identidades pitagóricas básicos para funciones trigonométricas Las identidades pitagóricas son bloques de construcción para muchas de las manipulaciones de ecuaciones y expresiones trigonométricas. Proporcionan un mayor número de métodos para resolver problemas trigonométricos de manera más eficiente, ya…
 Cotangente y cosecante identidades en un círculo unitario
Cotangente y cosecante identidades en un círculo unitario A partir de la identidad de Pitágoras, el pecado2theta- + cos2theta- = 1, puede derivar cotangente y cosecante identidades pitagóricas. Todo lo que hacemos es tirar un poco de álgebra y aplicar las identidades recíprocas y de relación y -…
 Tratar con identidades medio-ángulo que involucran radicales
Tratar con identidades medio-ángulo que involucran radicales Mediante la adición, sustracción, o duplicando medidas de los ángulos, se puede encontrar gran cantidad de valores exactos de las funciones trigonométricas. Por ejemplo, puede utilizar la identidad de medio ángulo cuando el valor exacto de la…
 Encuentra identidades relación trigonometría
Encuentra identidades relación trigonometría Trig tiene dos identidades llamados identidades de relación. Esta etiqueta puede ser confuso, ya que todas las funciones trigonométricas se definen por relaciones. En algún momento, sin embargo, los matemáticos pensaron que esta descripción era…
 ¿Cómo encontrar identidades medio-ángulo para tangente
¿Cómo encontrar identidades medio-ángulo para tangente La media de ángulo trig identidad para tangente tiene dos versiones. En lugar de que esto sea una molestia, que tiene más de una opción es realmente bastante agradable, porque se puede elegir la versión que mejor se adapte a su situación. Las…
 Cómo eliminar un tercer ángulo para resolver una identidad trigonometría
Cómo eliminar un tercer ángulo para resolver una identidad trigonometría Identidades de suma y diferencia por lo general implican dos ángulos diferentes y luego un tercer ángulo combinado. Al probar estas identidades trigonométricas, a menudo es necesario deshacerse de ese tercer ángulo. El siguiente ejemplo trata de…
 Cómo utilizar identidades medio ángulo para encontrar el seno de un ángulo
Cómo utilizar identidades medio ángulo para encontrar el seno de un ángulo Mediante la adición, sustracción, o duplicando medidas de los ángulos, se puede encontrar gran cantidad de valores exactos de las funciones trigonométricas utilizando las funciones de ángulos que ya conoce. Por ejemplo, a pesar de que se puede…
 Cómo utilizar la identidad de ángulo suma, cuando usted no sabe el ángulo
Cómo utilizar la identidad de ángulo suma, cuando usted no sabe el ángulo En algunos problemas de trigonometría, usted no puede saber lo que la medida de un ángulo es, pero usted sabe algo acerca de valores de la función del ángulo. Por ejemplo, suponga que tiene dos ángulos, alfa en el segundo cuadrante de un…
 Cómo utilizar las identidades de resta en un problema trig
Cómo utilizar las identidades de resta en un problema trig Usted puede encontrar valores de la función de los ángulos utilizando identidades ángulo de adición. Y usted tiene más posibilidades de encontrar los valores de la función de los ángulos cuando se utiliza la resta en un problema de…
 Identidades de producto a suma
Identidades de producto a suma Las identidades trigonométricas de producto a suma se parecen mucho. Hay que prestar mucha atención a las diferencias sutiles para que pueda aplicarlas correctamente. A pesar de que el producto se ve bonito y compacto, que no siempre es tan fácil…
 Identidades trigonométricas recíprocas
Identidades trigonométricas recíprocas El trig más simple y básica identidades (ecuaciones de equivalencia) son las que implican los inversos de las funciones trigonométricas. Para refrescar la memoria, un recíproco de un número es 1 dividido por el número - por ejemplo, el…