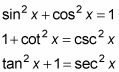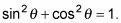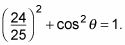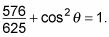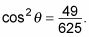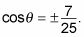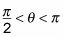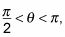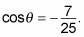¿Cómo encontrar funciones trigonométricas de un ángulo utilizando identidades pitagóricas
Puede utilizar identidades pitagóricas para encontrar la función trigonométrica de un ángulo si usted sabe de una función trigonométrica del ángulo y está buscando otro. Por ejemplo, si se conoce el seno de un ángulo, puede utilizar la primera identidad de Pitágoras para encontrar el coseno del ángulo. De hecho, usted puede encontrar lo que te pide de encontrar si todo lo que tienes es el valor de una función trigonométrica y la comprensión de lo cuadrante del ángulo # 952- es en.
Las tres identidades pitagóricas son
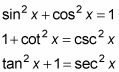
He aquí un ejemplo:
Si usted sabe que
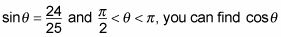
siguiendo estos pasos:
Plug lo que sabe sobre la identidad de Pitágoras apropiado.
Debido a que usted está utilizando seno y coseno, se utiliza la primera identidad:
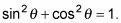
Enchufe los valores que sabe llegar
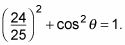
Aislar la función trigonométrica con la variable en un lado.
Primero cuadrar el valor del seno para obtener 576/625, dándole
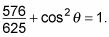
Reste 576/625 de ambos lados (Pista: Es necesario encontrar un denominador común):
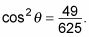
Figura la raíz cuadrada ambos lados (teniendo ambos las raíces cuadradas positivas y negativas) para resolver.
Ahora tiene
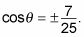
Pero usted puede tener sólo una solución debido a la restricción
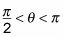
que te dan en el problema.
Haz un dibujo del círculo unidad para que pueda visualizar el ángulo.
Porque
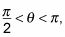
el ángulo se encuentra en el cuadrante II, por lo que el coseno de # 952- debe ser negativo. Usted tiene su respuesta:
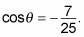
Sobre el autor
 ¿Cómo simplificar una expresión utilizando identidades periodicidad
¿Cómo simplificar una expresión utilizando identidades periodicidad Identidades Periodicidad ilustrar cómo trasladar la gráfica de una función trigonométrica por un período a los resultados de izquierda o derecha en la misma función. Las funciones de seno, coseno, secante, cosecante y repetir cada 2 (pi)…
 Cómo utilizar un ángulo de referencia para encontrar ángulos de soluciones
Cómo utilizar un ángulo de referencia para encontrar ángulos de soluciones En pre-cálculo, a usar funciones trigonométricas para resolver ecuaciones algebraicas. Cuando encuentre el valor del ángulo en una ecuación, que es el ángulo que es una solución a la ecuación, se utiliza que como el ángulo de referencia para…
 Cómo utilizar identidades medio ángulo para evaluar una función trigonométrica
Cómo utilizar identidades medio ángulo para evaluar una función trigonométrica Puede utilizar identidades-medio ángulo para evaluar una función trigonométrica de un ángulo que no está en el círculo unitario utilizando uno que sea. Por ejemplo, 15 grados, que no es en el círculo unitario, es la mitad de 30 grados, que se…
 Asignar valores de la función trigonométrica negativos y positivos por cuadrante
Asignar valores de la función trigonométrica negativos y positivos por cuadrante El primer paso para encontrar el valor de la función trigonométrica de uno de los ángulos que es un múltiplo de 30 o 45 grados es encontrar el ángulo de referencia en el círculo unitario. Cuando el ángulo de referencia viene a ser 0, 30, 45,…
 Tratar con identidades medio-ángulo que involucran radicales
Tratar con identidades medio-ángulo que involucran radicales Mediante la adición, sustracción, o duplicando medidas de los ángulos, se puede encontrar gran cantidad de valores exactos de las funciones trigonométricas. Por ejemplo, puede utilizar la identidad de medio ángulo cuando el valor exacto de la…
 Encuentra identidades trigonométricas opuesto ángulo
Encuentra identidades trigonométricas opuesto ángulo los identidades de ángulo opuesto cambiar las funciones trigonométricas de ángulos negativos a las funciones de ángulos positivos. Ángulos negativos son grandes para describir una situación, pero no son realmente útil cuando se trata de pegar…
 ¿Cómo encontrar identidades medio-ángulo para tangente
¿Cómo encontrar identidades medio-ángulo para tangente La media de ángulo trig identidad para tangente tiene dos versiones. En lugar de que esto sea una molestia, que tiene más de una opción es realmente bastante agradable, porque se puede elegir la versión que mejor se adapte a su situación. Las…
 Cómo localizar ángulos de referencia
Cómo localizar ángulos de referencia Cada uno de los ángulos en un círculo unidad tiene un ángulo de referencia, que es siempre un ángulo agudo positivo (excepto los ángulos que ya son positivas y aguda). Al identificar el ángulo de referencia, se puede determinar los valores de…
 ¿Cómo resolver funciones trigonométricas inversas con ángulos poco comunes
¿Cómo resolver funciones trigonométricas inversas con ángulos poco comunes Cuando se trabaja con funciones trigonométricas inversas, siempre es más conveniente cuando los números que está trabajando son los resultados de la aplicación de una de las funciones trigonométricas a una medida de ángulo común. Cuando el…
 Cómo utilizar identidades medio ángulo para encontrar el seno de un ángulo
Cómo utilizar identidades medio ángulo para encontrar el seno de un ángulo Mediante la adición, sustracción, o duplicando medidas de los ángulos, se puede encontrar gran cantidad de valores exactos de las funciones trigonométricas utilizando las funciones de ángulos que ya conoce. Por ejemplo, a pesar de que se puede…
 Cómo utilizar la identidad de ángulo suma, cuando usted no sabe el ángulo
Cómo utilizar la identidad de ángulo suma, cuando usted no sabe el ángulo En algunos problemas de trigonometría, usted no puede saber lo que la medida de un ángulo es, pero usted sabe algo acerca de valores de la función del ángulo. Por ejemplo, suponga que tiene dos ángulos, alfa en el segundo cuadrante de un…
 Cómo utilizar la identidad de doble ángulo para el seno
Cómo utilizar la identidad de doble ángulo para el seno La fórmula de doble ángulo para el seno proviene del uso de la identidad trigonométrica para el seno de una suma, el pecado (alfa + beta-) = sinalpha-cosbeta- +-cosalpha sinbeta-. Si alfa = beta-, entonces se puede sustituir beta- con alfa en la…