¿Cómo encontrar el seno de un ángulo de doblado

Se utiliza un fórmula de doble ángulo para encontrar el valor geodésico de doble ángulo. A veces se conoce el ángulo cerrado original, a veces no lo hace. Trabajar con fórmulas de doble ángulo es muy útil cuando se te da el seno de un ángulo y la necesidad de encontrar el valor exacto trig de dos veces ese ángulo sin conocer la medida del ángulo original.

Nota: Si conoce el ángulo original en cuestión, encontrando el seno del doble que el ángulo es de fácil puedes buscarlo en el círculo unidad (que se muestra en la figura) o utilizar la calculadora para encontrar la respuesta.

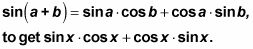
Sin embargo, si usted no tiene la medida del ángulo original y usted debe encontrar el valor exacto de dos veces ese ángulo, el proceso no es tan simple. Siga leyendo!

Para comprender y ser capaz de guardar lejos la fórmula de doble ángulo para el seno, primero debe entender de dónde viene. (Las fórmulas de doble ángulo de seno, coseno y tangente son muy diferentes entre sí, aunque todos ellos pueden ser derivadas por el uso de las fórmulas de suma.)

1. Para encontrar el pecado 2X, usted debe darse cuenta de que es el mismo que el pecado (X + X).

2. Utilice la fórmula suma de seno,

   

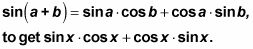
3. Simplifique para obtener

   

   Esta fórmula se llama fórmula de doble ángulo para el seno. Si te dan una ecuación con más de una función trigonométrica y pide que resolver para el ángulo, la mejor opción es la de expresar la ecuación en términos de una sola función trigonométrica. A menudo se puede lograr esto mediante el uso de la fórmula de doble ángulo.

Resolver

cuenta de que no es igual a 0, por lo que no se puede factorizar ella. Incluso si se resta 1 de ambos lados para obtener 0, todavía puede no tenerse en cuenta. Así que no hay solución, ¿no? No exactamente. Usted tiene que comprobar las identidades primero. La fórmula de doble ángulo, por ejemplo, dice que

Puede volver a escribir algunas cosas aquí:

1. Anote la información dada.

   Tienes

   

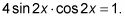
2. Vuelva a escribir la ecuación para encontrar una posible identidad.

   Vas con

   

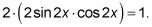
3. Aplicar la fórmula correcta.

   La fórmula de doble ángulo para el seno le da

   

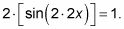
4. Simplifique la ecuación y aislar la función trigonométrica.

   Pierde el control de

   

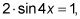
   que se convierte en pecado 4X = 1/2.

5. Encuentre todas las soluciones para la ecuación trigonométrica.

   Este paso le da

   

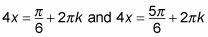
   dónde k es un número entero. Tenga en cuenta que hay dos conjuntos de soluciones porque sin (pi / 6) y sin (5pi / 6) ambos iguales # 189-. Se utiliza la notación

   

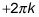
   para representar el hecho de que la función seno tiene un plazo de 2pi, lo que significa que se repite cada unidades 2pi. A continuación, puede dividir todo

   

   por 4, que le da las soluciones:

   

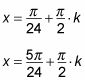
Estas soluciones son las generales, pero en algún momento puede que tenga que utilizar esta información para llegar a una solución en un intervalo.

Encontrar las soluciones en un intervalo es una curva lanzado en usted en pre-cálculo. Para este problema, usted puede encontrar un total de ocho ángulos en el intervalo [0, 2pi). Debido a un coeficiente estaba en frente de la variable, que te queda, en este caso, cuatro veces más soluciones, y debe indicar a todos. Tienes que encontrar el denominador común para agregar las fracciones.

Hacer esto una vez más le consigue

que no está en el intervalo [0, 2pi). Mientras tanto,

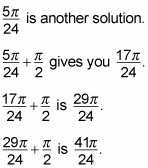
Dejas de allí, porque la adición de pi / 2, una vez más sería conseguir que una solución que no está en el intervalo [0, 2pi).