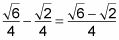Cómo calcular el seno de ángulos especiales en radianes
Usted puede utilizar el concepto de fórmulas de suma y diferencia para calcular el seno de ángulos especiales en radianes. Este proceso es diferente a la resolución de ecuaciones porque aquí se le pedirá que encontrar el valor trigonométrica de un ángulo específico que no se marcó fácilmente en el círculo unitario
Antes de elegir la fórmula adecuada, sólo tiene que romper el ángulo en cualquiera de la suma o la diferencia de dos ángulos del círculo unitario. Consulte el círculo unidad y observe los ángulos en radianes en la figura.
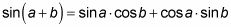
Usted ve que todos los denominadores son diferentes, lo que hace la suma y resta de ellos una pesadilla. Usted debe encontrar un denominador común para que sumar y restar es un sueño. El denominador común es 12, como se puede ver en la figura.
Esta cifra es muy útil sólo para las fórmulas de suma y diferencia, porque encontrar un denominador común es algo que sólo se hace cuando va a añadir o restar fracciones.
A modo de ejemplo, siga estos pasos para encontrar el valor exacto de sin (pi / 12):
Vuelva a escribir el ángulo en cuestión, utilizando los ángulos especiales en radianes con denominadores comunes.
A partir de la figura, que desea una forma de sumar o restar dos ángulos de manera que, al final, se obtiene pi / 12.
Elija la fórmula apropiada suma o diferencia:
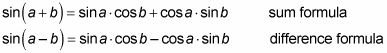
Debido a que reescribió el ángulo con la resta, es necesario utilizar la fórmula de diferencia.
Enchufe la información que usted sabe en la fórmula elegida.
Usted sabe la siguiente igualdad:
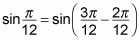
Sustituto de la siguiente manera en la fórmula de la diferencia:
¿Qué le da
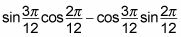
Reducir las fracciones en la fórmula a los que estás más cómodo.
En este ejemplo, se puede reducir a
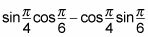
Ahora usted tendrá un tiempo más fácil referirse a la unidad de círculo para obtener su ecuación.
Use el círculo unitario para buscar los valores de seno y coseno que usted necesita.
Ahora tiene
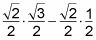
Multiplicar y simplificar para obtener su respuesta final.
Se termina con la siguiente respuesta:
-
La aplicación de las fórmulas de suma y diferencia de los cosenos para encontrar el coseno de la suma o diferencia de dos ángulos -
Cómo aplicar las fórmulas de suma y diferencia de coseno de trig pruebas -
Cómo calcular el seno de ángulos especiales en grados -
¿Cómo expresar sumas o diferencias de funciones trigonométricas como productos -
¿Cómo encontrar el seno de un ángulo de doblado -
¿Cómo encontrar la tangente de la suma o diferencia de ángulos
Cómo medir ángulos con radianes Grados no son la única forma de medir los ángulos. También puede utilizar radianes. Grados y radianes son sólo dos formas diferentes de medir ángulos, como pulgadas y centímetros son dos formas de medir la longitud.los radián medida de un…
Cómo utilizar identidades medio ángulo para evaluar una función trigonométrica Puede utilizar identidades-medio ángulo para evaluar una función trigonométrica de un ángulo que no está en el círculo unitario utilizando uno que sea. Por ejemplo, 15 grados, que no es en el círculo unitario, es la mitad de 30 grados, que se…
Definir el radián en la trigonometría Introducción de una persona para ángulos es por lo general en términos de grados. Es probable que tenga una buena idea de lo que es un ángulo de 45 grados se parece. E incluso la mayoría de los estudiantes de secundaria saben que un triángulo…
Cómo determinar la medida de un ángulo cuyo vértice se encuentra fuera de un círculo Un ángulo que cruza un círculo puede tener su vértice en el interior, sobre o fuera del círculo. Este artículo aborda los tres tipos de ángulos que tienen sus vértices fuera de un círculo: ángulos secante-secantes, ángulos…
Encontrar la función de la trigonometría de un ángulo en un círculo unitario Puede determinar las funciones trigonométricas de cualquier ángulo que se encuentran en el círculo unitario - cualquiera que se grafican en posición estándar (es decir, el vértice del ángulo está en el origen, y el lado inicial se encuentra…
Cómo localizar ángulos de referencia Cada uno de los ángulos en un círculo unidad tiene un ángulo de referencia, que es siempre un ángulo agudo positivo (excepto los ángulos que ya son positivas y aguda). Al identificar el ángulo de referencia, se puede determinar los valores de…
Cómo eliminar un tercer ángulo para resolver una identidad trigonometría Identidades de suma y diferencia por lo general implican dos ángulos diferentes y luego un tercer ángulo combinado. Al probar estas identidades trigonométricas, a menudo es necesario deshacerse de ese tercer ángulo. El siguiente ejemplo trata de…
Cómo utilizar la identidad de ángulo suma, cuando usted no sabe el ángulo En algunos problemas de trigonometría, usted no puede saber lo que la medida de un ángulo es, pero usted sabe algo acerca de valores de la función del ángulo. Por ejemplo, suponga que tiene dos ángulos, alfa en el segundo cuadrante de un…
Cómo utilizar la identidad de doble ángulo para el seno La fórmula de doble ángulo para el seno proviene del uso de la identidad trigonométrica para el seno de una suma, el pecado (alfa + beta-) = sinalpha-cosbeta- +-cosalpha sinbeta-. Si alfa = beta-, entonces se puede sustituir beta- con alfa en la…
Cómo utilizar las identidades de resta en un problema trig Usted puede encontrar valores de la función de los ángulos utilizando identidades ángulo de adición. Y usted tiene más posibilidades de encontrar los valores de la función de los ángulos cuando se utiliza la resta en un problema de…
Los ángulos positivos y negativos en un círculo unitario El círculo unidad es una plataforma para la descripción de todas las posibles medidas de los ángulos de 0 a 360 grados, todos los negativos de esos ángulos, además de todos los múltiplos de los ángulos positivos y negativos de menos infinito…
Identidades de producto a suma Las identidades trigonométricas de producto a suma se parecen mucho. Hay que prestar mucha atención a las diferencias sutiles para que pueda aplicarlas correctamente. A pesar de que el producto se ve bonito y compacto, que no siempre es tan fácil…