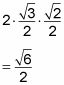¿Cómo expresar sumas o diferencias de funciones trigonométricas como productos
Es una buena idea familiarizarse con un conjunto de fórmulas que cambian sumas a los productos. Fórmulas de suma a producto son útiles para ayudarle a encontrar la suma de dos valores trigonométricas que no están en el círculo unitario. Por supuesto, estas fórmulas funcionan sólo si la suma o diferencia de los dos ángulos termina siendo un ángulo desde los triángulos especiales:

Aquí están las identidades suma / diferencia a producto:
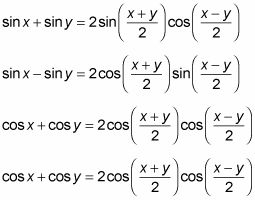
Por ejemplo, digamos que usted le pide que encuentre
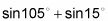
sin una calculadora. Usted está atascado, ¿verdad? Bueno, no exactamente. Debido a que se le pide que encontrar la suma de dos funciones trigonométricas cuyos ángulos no son ángulos especiales, puede cambiar a un producto mediante la suma de las fórmulas de productos. Sigue estos pasos:
Cambie la suma a un producto.
Debido a que se le pide que encontrar la suma de dos funciones seno, utilice esta ecuación:
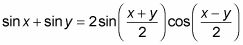
Este paso le da
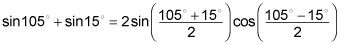
Simplificar el resultado.
Combinando términos semejantes y divisoria le da
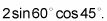
Estos ángulos están representados en el círculo unidad, por lo que continúan con el siguiente paso.
El círculo unidad entera
Use el círculo unitario para simplificar aún más.

Sustituyendo estos valores en, se obtiene
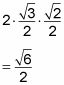
Sobre el autor
 ¿Cómo expresar productos de funciones trigonométricas como sumas o diferencias
¿Cómo expresar productos de funciones trigonométricas como sumas o diferencias Si usted puede romper un producto de funciones trigonométricas en la suma de dos términos diferentes, cada uno con su propia función trigonométrica, hacer los cálculos se vuelve mucho más fácil. En pre-cálculo, problemas de este tipo suelen…
 ¿Cómo encontrar la tangente de la suma o diferencia de ángulos
¿Cómo encontrar la tangente de la suma o diferencia de ángulos Al igual que con seno y coseno, usted puede confiar en fórmulas para encontrar la tangente de una suma o una diferencia de ángulos. La principal diferencia es que no se puede leer tangentes directamente de las coordenadas de los puntos en el…
 Cómo utilizar un ángulo de referencia para encontrar ángulos de soluciones
Cómo utilizar un ángulo de referencia para encontrar ángulos de soluciones En pre-cálculo, a usar funciones trigonométricas para resolver ecuaciones algebraicas. Cuando encuentre el valor del ángulo en una ecuación, que es el ángulo que es una solución a la ecuación, se utiliza que como el ángulo de referencia para…
 Cómo utilizar identidades medio ángulo para evaluar una función trigonométrica
Cómo utilizar identidades medio ángulo para evaluar una función trigonométrica Puede utilizar identidades-medio ángulo para evaluar una función trigonométrica de un ángulo que no está en el círculo unitario utilizando uno que sea. Por ejemplo, 15 grados, que no es en el círculo unitario, es la mitad de 30 grados, que se…
 Pre-cálculo para dummies
Pre-cálculo para dummies En pre-cálculo, el círculo unitario es algo así como calles de la unidad, es el círculo muy pequeño en un gráfico que abarca las coordenadas 0,0. Tiene un radio de 1, por lo tanto la unidad. La figura muestra aquí todas las mediciones de la…
 Problemas de la práctica de la geometría con triángulos y polígonos
Problemas de la práctica de la geometría con triángulos y polígonos LA polígono es una figura geométrica que tiene al menos tres lados. El triángulo es el polígono más básico. Usted encontrará las siguientes fórmulas y propiedades útiles al responder a las preguntas que implican desigualdades triángulo,…
 Fórmulas de geometría que usted debe saber
Fórmulas de geometría que usted debe saber A continuación se presentan algunas de las fórmulas de geometría más importantes, teoremas, propiedades, etc. que se utilizan para resolver diversos problemas. Si te quedas perplejo mientras se trabaja en un problema y no puede llegar a una…
 Cómo calcular funciones trigonométricas usando cualquier círculo
Cómo calcular funciones trigonométricas usando cualquier círculo Cuando la determinación de los valores de la función trigonométrica de ángulos graficadas en la posición estándar en un círculo cuyo centro está en el origen, usted no tiene que tener un círculo unitario para calcular coordenadas. Puede…
 Cómo calcular las funciones trigonométricas de ángulos usando el círculo unitario
Cómo calcular las funciones trigonométricas de ángulos usando el círculo unitario Cálculo de funciones trigonométricas de ángulos dentro de un círculo unidad es muy fácil. La figura muestra un círculo unitario, que tiene la ecuación X2 + y2 = 1, junto con algunos puntos de la circunferencia y sus coordenadas.El uso de los…
 Cómo eliminar un tercer ángulo para resolver una identidad trigonometría
Cómo eliminar un tercer ángulo para resolver una identidad trigonometría Identidades de suma y diferencia por lo general implican dos ángulos diferentes y luego un tercer ángulo combinado. Al probar estas identidades trigonométricas, a menudo es necesario deshacerse de ese tercer ángulo. El siguiente ejemplo trata de…
 Cómo utilizar la identidad de ángulo suma, cuando usted no sabe el ángulo
Cómo utilizar la identidad de ángulo suma, cuando usted no sabe el ángulo En algunos problemas de trigonometría, usted no puede saber lo que la medida de un ángulo es, pero usted sabe algo acerca de valores de la función del ángulo. Por ejemplo, suponga que tiene dos ángulos, alfa en el segundo cuadrante de un…
 Identidades de producto a suma
Identidades de producto a suma Las identidades trigonométricas de producto a suma se parecen mucho. Hay que prestar mucha atención a las diferencias sutiles para que pueda aplicarlas correctamente. A pesar de que el producto se ve bonito y compacto, que no siempre es tan fácil…
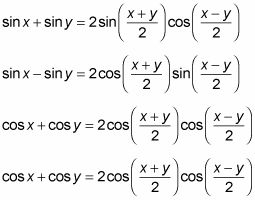
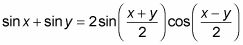
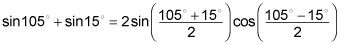
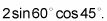
 El círculo unidad entera
El círculo unidad entera