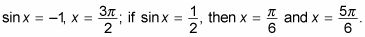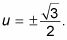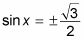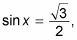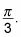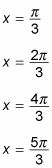¿Cómo combinar los ángulos de referencia con otras técnicas para resolver ecuaciones trigonométricas

categoría Educación y lenguas / Matemáticas / Cálculo

Puede incorporar ángulos de referencia en algunas otras técnicas de pre-cálculo para resolver ecuaciones trigonométricas. Una de estas técnicas es el factoring. Usted ha estado factoring desde álgebra, por lo que este proceso no debe ser nada nuevo. Cuando nos enfrentamos a una ecuación que es igual a 0 y una función trigonométrica que se está cuadrado, o si tiene dos funciones trigonométricas diferentes que están siendo multiplicados juntos, usted debe tratar de utilizar el factoring para obtener su solución de primera. Después de factoraje, puede utilizar la propiedad del producto cero para ajustar cada factor igual a 0 y luego resolverlos por separado.

Intenta resolver un ejemplo que involucra factorizar un trinomio pecado 22 X + pecado X - 1 = 0 utilizando los siguientes pasos:

  1. Deje una variable igual a la relación trigonométrica y reescribir la ecuación para simplificar.

    Dejar u = Sen X y volver a escribir la ecuación como 2u2 + u - 1 = 0.

  2. Asegúrese de que los factores de la ecuación.

    Recuerde revisar siempre para el factor máximo común primero.

  3. Factor de la cuadrática.

    La ecuación 2u2 + u - 1 = 0 factores a (u + 1) (2u - 1) = 0.

  4. Cambie las variables de nuevo a las funciones trigonométricas.

    Reescribiendo la ecuación trigonométrica factorizado le da (el pecado X + 1) (2 sen X - 1) = 0.

  5. Utilice la propiedad del producto cero a resolver.

    Si el pecado X + 1 = 0, entonces el pecado X = -1. Si 2sin X - 1 = 0, entonces el pecado X = 1/2. Por Consiguiente,

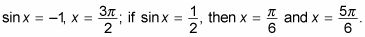
    image0.jpg

En pre-cálculo, es posible que tenga que tomar la raíz cuadrada de ambos lados para resolver una función de trigonometría. Por ejemplo, si te dan una ecuación como 4 pecado2 X - 3 = 0, siga estos pasos:

  1. Deje una variable igual a la expresión trigonométrica y reescribir la ecuación para simplificar.

    Dejar u = Sen X y volver a escribir la ecuación como 4u2 - 3 = 0.

  2. Aislar la expresión trigonométrica.

    Para 4u2 - 3 = 0, agregue 3 a cada lado y dividir por 4 a ambos lados para obtener u2 = 3/4.

  3. Toma la raíz cuadrada de ambos lados.

    No se olvide de tomar las raíces cuadradas positivas y negativas, que le da

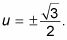
    image1.jpg

  4. Cambie las variables de nuevo a las funciones trigonométricas.

    Reescribiendo la ecuación trigonométrica factorizado le da

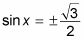
    image2.jpg

  5. Resuelva para encontrar el ángulo de referencia.

    El seno de X es tanto positiva como negativa para este ejemplo, lo que significa que las soluciones, o ángulos, están en los cuatro cuadrantes. Las soluciones son positivos en los cuadrantes I y II, y las soluciones negativos son en los cuadrantes III y IV. Utilice el ángulo de referencia en el cuadrante I a guiarte a las cuatro soluciones.

    Si

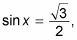
    image3.jpg

    el y valor en el primer cuadrante es el largo de la pierna del triángulo 30-60-90 grados. Por lo tanto, el ángulo de referencia es

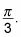
    image4.jpg

  6. Encuentre las soluciones.

    Utilice el ángulo de referencia para encontrar las cuatro soluciones:

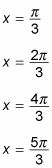
    image5.jpg

    Tenga en cuenta que dos de estas soluciones provienen del valor positivo de seno y dos vienen desde el valor negativo de sinusoidal.



Artículos Relacionados

Sobre el autor
Cómo utilizar identidades medio ángulo para evaluar una función trigonométrica Cómo utilizar identidades medio ángulo para evaluar una función trigonométrica

Puede utilizar identidades-medio ángulo para evaluar una función trigonométrica de un ángulo que no está en el círculo unitario utilizando uno que sea. Por ejemplo, 15 grados, que no es en el círculo unitario, es la mitad de 30 grados, que se…

Asignar valores de la función trigonométrica negativos y positivos por cuadrante Asignar valores de la función trigonométrica negativos y positivos por cuadrante

El primer paso para encontrar el valor de la función trigonométrica de uno de los ángulos que es un múltiplo de 30 o 45 grados es encontrar el ángulo de referencia en el círculo unitario. Cuando el ángulo de referencia viene a ser 0, 30, 45,…

Cómo factorizar expresiones trigonométricas por agrupación Cómo factorizar expresiones trigonométricas por agrupación

El proceso de factoring mediante la agrupación de las obras en casos muy especiales, cuando la expresión trigonometría original es el resultado de multiplicar dos binomios juntos que tienen algunos términos no relacionados en ellos.…

Cómo factorizar expresiones trigonométricas con títulos superiores a 2 Cómo factorizar expresiones trigonométricas con títulos superiores a 2

Aunque factoring cuadráticas es una brisa, factoring ecuaciones de trigonometría con grados más altos pueden ser un poco desagradable si usted no tiene una situación agradable, como sólo dos términos o una ecuación de segundo grado similar. A…

¿Cómo encontrar una solución a una ecuación trigonométrica de múltiples ángulos ¿Cómo encontrar una solución a una ecuación trigonométrica de múltiples ángulos

Expresiones trigonometría múltiple de ángulo son aquellos en los que la medida del ángulo es algún múltiplo de una variable - por ejemplo, 2X o 3y. Usted puede tomar estas expresiones separadas y despejar todas las soluciones adicionales que…

¿Cómo encontrar la inversa de una función trigonométrica ¿Cómo encontrar la inversa de una función trigonométrica

Utilice las funciones trigonométricas inversas para resolver ecuaciones como pecado X = 1/2, sec X = -2, O moreno 2X = 1. En las ecuaciones típicas de álgebra, puede resolver por el valor de X dividiendo cada lado de la ecuación por el…

Cómo localizar ángulos de referencia Cómo localizar ángulos de referencia

Cada uno de los ángulos en un círculo unidad tiene un ángulo de referencia, que es siempre un ángulo agudo positivo (excepto los ángulos que ya son positivas y aguda). Al identificar el ángulo de referencia, se puede determinar los valores de…

Cómo multiplicar a través de una ecuación trigonométrica con otra función Cómo multiplicar a través de una ecuación trigonométrica con otra función

La técnica de multiplicar a través de una ecuación de trigonometría por una función selecta no debe ser su primera opción - o su segunda, tercera o cuarta opción. Este método suele ser el último recurso. No es que el método es…

¿Cómo resolver una ecuación de trigonometría utilizando la fórmula cuadrática ¿Cómo resolver una ecuación de trigonometría utilizando la fórmula cuadrática

Cuando el factor trigonometría ecuaciones de segundo grado, la vida es buena. Cuando no lo hacen, usted todavía puede sobrevivir, gracias a que la fórmula cuadrática maravilloso. En caso de que hayas olvidado la fórmula exacta, aquí está.La…

¿Cómo resolver una ecuación de trigonometría factorizando cuadráticas ¿Cómo resolver una ecuación de trigonometría factorizando cuadráticas

Ecuaciones cuadráticas son agradables de trabajar porque, cuando no factor, puede resolverlos mediante el uso de la fórmula cuadrática. Los tipos de ecuaciones trigonométricas cuadráticas que puede factores son los que, como bronceado2 X = Tan…

¿Cómo resolver una ecuación trigonométrica que tiene múltiples funciones trigonométricas ¿Cómo resolver una ecuación trigonométrica que tiene múltiples funciones trigonométricas

Algunas ecuaciones de trigonometría contienen más de una función trigonométrica. Otros tienen mezclas de múltiples ángulos y ángulos individuales con la misma variable. Algunos ejemplos de tales ecuaciones incluyen 3cos2 X = Sen2 X, 2 seg X =…

¿Cómo resolver funciones trigonométricas inversas con ángulos poco comunes ¿Cómo resolver funciones trigonométricas inversas con ángulos poco comunes

Cuando se trabaja con funciones trigonométricas inversas, siempre es más conveniente cuando los números que está trabajando son los resultados de la aplicación de una de las funciones trigonométricas a una medida de ángulo común. Cuando el…

» » » » ¿Cómo combinar los ángulos de referencia con otras técnicas para resolver ecuaciones trigonométricas