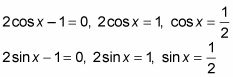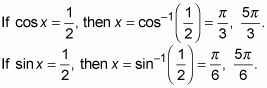Cómo factorizar expresiones trigonométricas por agrupación
El proceso de factoring mediante la agrupación de las obras en casos muy especiales, cuando la expresión trigonometría original es el resultado de multiplicar dos binomios juntos que tienen algunos términos no relacionados en ellos. Generalmente, usted puede aplicar este tipo de factoraje cuando te enfrentas a un número par de términos y puede encontrar factores comunes en los diferentes grupos de ellos.
Los tipos de ecuaciones que se pueden resolver mediante el uso de agrupación parecen 4sin X cos X - 2sin X - 2cos X + 1 = 0 o el pecado2 X segundo X + 2sin2 X = Sec X + 2. En la primera ecuación, los dos primeros términos tienen un factor común obvio, 2sin2 X. El segundo dos tienen ningún factor común que no sea 1, pero para hacer que agrupa el trabajo, se le factorizar -1.
Resuelva 4sin X cos X - 2sin X - 2cos X + 1 = 0 para todas las respuestas posibles entre 0 y 2pi-.
2sin Factor X fuera de los dos primeros términos y -1 fuera de la segunda dos.
2sin X (2cos X - 1) - 1 (2cos X - 1) = 0
Ahora usted tiene dos términos, cada uno con un factor de 2cos X - 1.
Factor que el factor común de los dos términos.
(2cos X - 1) (2sin X - 1) = 0
Ajuste los dos factores iguales a 0.
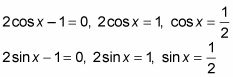
Resuelva para los valores de X que satisfacen la ecuación.
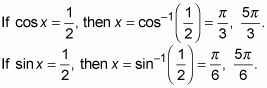
El siguiente ejemplo de agrupación requiere que usted comience moviendo los dos términos a la derecha hacia la izquierda. Otro giro es que uno de los factores resultantes resulta ser un cuadrática. ¿Cómo puede la Matemática ser mucho más divertido que esto?
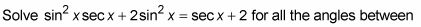
0 y 360 grados.
Mueva los términos de la derecha a la izquierda restando ellos desde ambos lados.
pecado2 X segundo X + 2sin2 X - segundo X - 2 = 0
Pecado Factor2 X fuera de los dos primeros términos y -1 fuera de la segunda dos.
pecado2 X (sec X + 2) - 1 (seg X + 2) = 0
Ahora el factor seg X + 2 de los dos términos.
(sec X + 2) (sen2 X - 1) = 0
Ajuste los dos factores iguales a 0.
segundo X + 2 = 0, sec X = -2
pecado2 X - 1 = 0, el pecado2 X = 1, el pecado X = 1 cuando se toma la raíz cuadrada de ambos lados.
Resuelva para los valores de X que satisfacen las ecuaciones.
Si seg X = -2, Entonces X = Sec-1(-2) = 120 # 186-, 186- # 240.
Si el pecado X = 1, entonces X = Sen-1(1) = 90 # 186-.
Si el pecado X = -1, Entonces X = Sen-1(-1) = 270 # 186-.
Cómo agrupar seis términos de factoring Puede agrupar términos de factoring en las expresiones en los términos no comparten un factor común o variable común. Cuando la agrupación de seis términos de factoraje, está la posibilidad de que los grupos pueden ser de dos grupos de tres…
Cómo desigual grupo de cuatro términos de factoring A veces, en factoring, cuatro términos se pueden separar en grupos irregulares con tres términos en un grupo y un término en el otro. Desigualmente agrupar cuatro términos para el factoring se pueden aplicar a las expresiones donde las…
Factoring cuatro o más términos agrupando Cuando un polinomio tiene cuatro o más términos, la forma más fácil de factorizar que es usar agrupación. En este método, nos fijamos en sólo dos términos a la vez para ver si cualquiera de las técnicas se hacen evidentes. Por ejemplo,…
¿Cómo combinar los ángulos de referencia con otras técnicas para resolver ecuaciones trigonométricas Puede incorporar ángulos de referencia en algunas otras técnicas de pre-cálculo para resolver ecuaciones trigonométricas. Una de estas técnicas es el factoring. Usted ha estado factoring desde álgebra, por lo que este proceso no debe ser nada…
Cómo factorizar expresiones matemáticas A menudo se necesita factor expresiones (rompen esas expresiones en sus componentes más simples, o factores) Para el cálculo. Medios de factoring " unmultiplying, " como la reescritura de 12 comoNo encuentras con problemas como que en el cálculo,…
Cómo utilizar el método de papel de aluminio para factorizar un trinomio Para polinomios con un coeficiente de liderazgo no preferenciales y término constante, se puede usar un procedimiento llamado Método FOIL de factoring (a veces llamado el Método británica). El método FOIL siempre trabaja para factorizar…
Cómo factorizar expresiones trigonométricas con títulos superiores a 2 Aunque factoring cuadráticas es una brisa, factoring ecuaciones de trigonometría con grados más altos pueden ser un poco desagradable si usted no tiene una situación agradable, como sólo dos términos o una ecuación de segundo grado similar. A…
Cómo multiplicar a través de una ecuación trigonométrica con otra función La técnica de multiplicar a través de una ecuación de trigonometría por una función selecta no debe ser su primera opción - o su segunda, tercera o cuarta opción. Este método suele ser el último recurso. No es que el método es…
¿Cómo resolver una ecuación de trigonometría utilizando la fórmula cuadrática Cuando el factor trigonometría ecuaciones de segundo grado, la vida es buena. Cuando no lo hacen, usted todavía puede sobrevivir, gracias a que la fórmula cuadrática maravilloso. En caso de que hayas olvidado la fórmula exacta, aquí está.La…
¿Cómo resolver una ecuación de trigonometría factorizando cuadráticas Ecuaciones cuadráticas son agradables de trabajar porque, cuando no factor, puede resolverlos mediante el uso de la fórmula cuadrática. Los tipos de ecuaciones trigonométricas cuadráticas que puede factores son los que, como bronceado2 X = Tan…
¿Cómo resolver una ecuación trigonométrica que tiene múltiples funciones trigonométricas Algunas ecuaciones de trigonometría contienen más de una función trigonométrica. Otros tienen mezclas de múltiples ángulos y ángulos individuales con la misma variable. Algunos ejemplos de tales ecuaciones incluyen 3cos2 X = Sen2 X, 2 seg X =…
Cómo cuadrar ambos lados de una ecuación trigonométrica Cuando la resolución de ecuaciones de trigonometría, más de un método generalmente funciona - a pesar de un método es a menudo más rápido o más fácil que otro. Con la práctica, usted obtendrá buenos en la elección de la mejor de las…