¿Cómo resolver una ecuación de trigonometría factorizando cuadráticas

Ecuaciones cuadráticas son agradables de trabajar porque, cuando no factor, puede resolverlos mediante el uso de la fórmula cuadrática. Los tipos de ecuaciones trigonométricas cuadráticas que puede factores son los que, como bronceado² X = Tan X, 4cos² X - 3 = 0, 2sin² X + 5sin X - 3 = 0, y csc² X + csc X - 2 = 0. Tenga en cuenta que todos ellos tienen la función de trigonometría revelador planteado el segundo grado. Los siguientes ejemplos muestran cómo manejarlos.

Los dos primeros ejemplos tienen sólo dos términos. Uno tiene dos términos variables, y el otro tiene una sola variable de plazo. En el primer ejemplo, se pone tanto en términos de la izquierda y luego factorizar el término variable o trig.

Resuelva bronceado² X = Tan X para los valores de X tal que 0 X lt; 2.

1. Mueva el término de la derecha a la izquierda de restarlo de ambos lados.

   bronceado² X - bronceado X = 0

   No divida a través de bronceado X. Vas a perder soluciones.

2. Factorizar bronceado X.

   bronceado X (bronceado X - 1) = 0

3. Ajuste cada uno de los dos factores iguales a 0.

   bronceado X = 0 o marrón X - 1 = 0

4. Resuelva para los valores de X que satisfacen ambas ecuaciones.

   Si bronceado X = 0, entonces X = Tan^-1(0) = 0,.

   

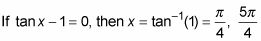
En el siguiente ejemplo, el binomio no factorizar fácilmente como la diferencia de dos cuadrados, ya que el 3 no es un cuadrado perfecto, y usted tiene que utilizar un radical en la factorización. Una manera agradable, eficiente para resolver esta ecuación es mover la 3 a la derecha y tomar la raíz cuadrada de cada lado.

Resuelva todas las posibles soluciones de 4cos² X - 3 = 0 en grados.

1. Mueva el número a la derecha mediante la adición de 3 a cada lado.

   4cos² X = 3

2. Divide cada lado por 4, y luego tomar la raíz cuadrada de cada lado para resolver cos X.

   

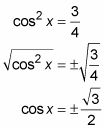
3. Resuelva las dos ecuaciones para los valores de X.

   

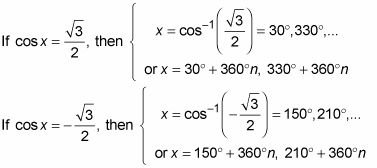
   Si tenemos en cuenta todos los múltiplos de 360 ​​grados añadidos a los cuatro ángulos de la base, usted encontrará que esta ecuación tiene montones y montones de soluciones.

Los siguientes dos ejemplos implican el uso de un-FOIL - una técnica para determinar el producto de dos binomios que le da un trinomio de segundo grado en particular. A veces, cuando se oscurece el patrón en el trinomio, es posible que desee sustituir primero alguna otra variable para la función trigonométrica para ayudar a determinar cómo se toma la misma. En este ejemplo, esto se hace para resolver 2sin² X + 5sin X - 3 = 0 para todos los valores de X entre 0 y 360 grados.

1. Sustituya cada pecado X con y.

   2y² + 5y - 3 = 0

2. Factorizar el trinomio como el producto de dos binomios.

   (2y - 1) (y + 3) = 0

3. Sustituya cada y con el pecado X.

   (2sin X - 1) (sen X + 3) = 0

4. Ajuste cada factor igual a 0.

   2sin X - 1 = 0 o el pecado X + 3 = 0

5. Resuelva las dos ecuaciones para los valores de X que satisfacen ellos.

   

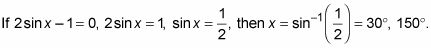
   Si el pecado X + 3 = 0, el pecado X = -3, Entonces X = Sen^-1(-3). Este resultado no tiene sentido, debido a que la función seno sólo produce valores entre -1 y 1 - lo que este factor no produce ninguna solución.

   Las dos únicas soluciones son 30 y 150 grados.

El siguiente ejemplo factores con bastante facilidad, pero se trata de una función recíproca. Resuelva csc² X + csc X - 2 = 0 para cualquier ángulo entre 0 y 2# 112- radianes.

1. Factorizar el trinomio de segundo grado en el producto de dos binomios.

   (csc X + 2) (csc X - 1) = 0

2. Ajuste cada factor igual a 0.

   csc X + 2 = 0 o csc X - 1 = 0

3. Resuelva las dos ecuaciones para los valores de X que satisfacen ellos.

   

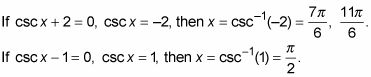
   Una forma alternativa de tratar con estas dos ecuaciones binomiales es cambiarlos usando la identidad recíproca y escribir el recíproco del número. Por primera ecuación, que te cambia de cosecante de seno:

   

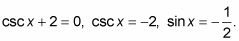
   Haga lo mismo con la segunda ecuación: csc X - 1 = 0, csc X = 1, el pecado X = 1. Se podría entonces resolver las ecuaciones inversas.