Reorganizar las identidades pitagóricas
Familiarizarse con las diferentes versiones de las identidades pitagóricas es útil para que pueda reconocer fácilmente en la resolución de ecuaciones de trigonometría o simplificar expresiones.
Conteúdo
Todas estas diferentes versiones tienen sus establecimientos en aplicaciones trigonométricas, cálculo, u otros temas de matemáticas. Usted no tiene que memorizar, porque si sólo recuerda las tres identidades pitagóricas, puede resolver por lo que necesita.
Cambiar el pecado2theta- + cos2theta- = 1
Usted puede alterar la identidad pitagórica original, en miles de formas. Para empezar, puede aislar bien el pecado2theta- o cos2theta- en un lado de la ecuación restando el otro término:
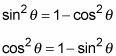
Continuando, usted puede factorizar el lado derecho de cada una de estas ecuaciones, porque ese lado es la diferencia de dos cuadrados perfectos:
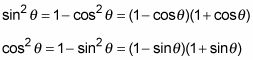
A veces, sin embargo, tener una expresión para sintheta- o costheta-, donde las funciones no son cuadrados, es de gran ayuda. A partir de la identidad pitagórica de base, cuando una función es por sí mismo, usted puede tomar la raíz cuadrada de cada lado para obtener
Ajuste de bronceado2theta- + 1 = sec2theta-
También puede adaptar esta segunda identidad de Pitágoras de varias maneras. Despejando bronceado2theta- restando 1 de cada lado de la ecuación, se obtiene
Entonces, la factorización de la diferencia de los cuadrados de la derecha (porque ese lado es la diferencia de dos cuadrados perfectos), tiene
Por último, a partir de la versión anterior y tomando la raíz cuadrada de cada lado, se obtiene
Tomando otro enfoque de esta identidad pitagórica, puede restar bronceado2 de cada lado y factorizar el resultado para obtener
Reconfiguración 1 + cuna2theta- = csc2theta-
Puede reorganizar la última identidad de Pitágoras, también, restando 1 de cada lado o por cuna restando2theta- de cada lado. Las dos nuevas versiones
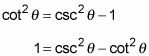
Cada una de las ecuaciones anteriores tiene la diferencia de dos cuadrados perfectos, que se puede Factor:
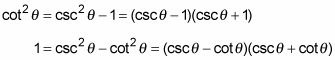
Y, por último, la raíz cuadrada de cada lado da una identidad que implica simplemente cottheta-:
-
Cómo factorizar la diferencia de dos cuadrados perfectos -
Primeros pasos con identidades trigonométricas -
Cómo factorizar una diferencia de cuadrados -
¿Cómo encontrar funciones trigonométricas de un ángulo utilizando identidades pitagóricas -
¿Cómo demostrar una identidad trigonométrica que contiene una raíz cuadrada -
¿Cómo demostrar una igualdad usando identidades pitagóricas
¿Cómo simplificar una expresión utilizando par / impar identidades Debido seno, coseno, y la tangente son funciones (funciones trigonométricas), que pueden definirse como pares o impares funciones. Sine y la tangente son funciones impares, y el coseno es una función par. En otras palabras,pecado(-X) = -sen Xcos…
Descubriendo ternas pitagóricas El teorema de Pitágoras es sin duda uno de los teoremas más famosos de toda la matemática. Matemáticos y laicos por igual han estudiado durante siglos, y la gente ha demostrado de muchas maneras diferentes. (Incluso el presidente James Garfield…
Identidades pitagóricas básicos para funciones trigonométricas Las identidades pitagóricas son bloques de construcción para muchas de las manipulaciones de ecuaciones y expresiones trigonométricas. Proporcionan un mayor número de métodos para resolver problemas trigonométricos de manera más eficiente, ya…
Cotangente y cosecante identidades en un círculo unitario A partir de la identidad de Pitágoras, el pecado2theta- + cos2theta- = 1, puede derivar cotangente y cosecante identidades pitagóricas. Todo lo que hacemos es tirar un poco de álgebra y aplicar las identidades recíprocas y de relación y -…
Sine Express en términos de coseno A pesar de que cada función de la trigonometría es perfectamente maravilloso, poder expresar cada función trig en términos de una de las otras cinco funciones trigonométricas es con frecuencia a su ventaja. Por ejemplo, usted puede tener…
Cómo eliminar un tercer ángulo para resolver una identidad trigonometría Identidades de suma y diferencia por lo general implican dos ángulos diferentes y luego un tercer ángulo combinado. Al probar estas identidades trigonométricas, a menudo es necesario deshacerse de ese tercer ángulo. El siguiente ejemplo trata de…
¿Cómo resolver una ecuación de trigonometría factorizando cuadráticas Ecuaciones cuadráticas son agradables de trabajar porque, cuando no factor, puede resolverlos mediante el uso de la fórmula cuadrática. Los tipos de ecuaciones trigonométricas cuadráticas que puede factores son los que, como bronceado2 X = Tan…
¿Cómo resolver una ecuación trigonométrica que tiene múltiples funciones trigonométricas Algunas ecuaciones de trigonometría contienen más de una función trigonométrica. Otros tienen mezclas de múltiples ángulos y ángulos individuales con la misma variable. Algunos ejemplos de tales ecuaciones incluyen 3cos2 X = Sen2 X, 2 seg X =…
Cómo cuadrar ambas partes para resolver un problema de identidad trigonometría Cuando se trabaja en ambos lados de una identidad trigonométrica, al mismo tiempo, es posible que a veces tenga que cuadrar ambos lados. Por lo general, utilizar esta técnica cuando un lado o el otro (o ambos) tiene un radical. Este método…
¿Cómo trabajar ambos lados de una identidad trig Con una identidad trigonometría, trabajando en ambos lados de la ecuación es aún más divertido que trabajar en ambos lados de una algebraico ecuación. En álgebra, puede multiplicar cada lado por el mismo número, cuadrado ambos lados, añadir…
Identificar ternas pitagóricas comunes LA Pitágoras triples es una lista de tres números que trabaja en el teorema de Pitágoras - el cuadrado del número más grande es igual a la suma de los cuadrados de los dos números más pequeños. El múltiplo de cualquier terna pitagórica…
La identificación de propiedades algebraicas más utilizados en la resolución de identidades Resolución de identidades es casi un rito de paso para los que estudian trigonometría. Hacer frente a la perspectiva de la resolución de identidades - y más tarde simplificar expresiones trigonométricas en cálculo - va mucho más suavemente si…