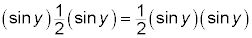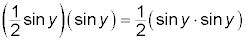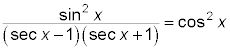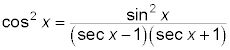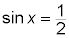La identificación de propiedades algebraicas más utilizados en la resolución de identidades
Resolución de identidades es casi un rito de paso para los que estudian trigonometría. Hacer frente a la perspectiva de la resolución de identidades - y más tarde simplificar expresiones trigonométricas en cálculo - va mucho más suavemente si usted tiene algunas herramientas algebraicas en la mano. Con un plan de acción, podrás tener éxito más rápida y eficiente y tener el producto deseado.
Al resolver una identidad, usted traer algunas sustituciones trigonométricas (identidades básicas, tales como el pecado2 X + cos2 X = 1), pero todo el trabajo tiene su principal base en las normas y técnicas algebraicas. Estas son las propiedades algebraicas que se encuentran con mayor frecuencia cuando se trabaja con identidades:
Propiedad conmutativa de la suma y la multiplicación: 2 sen X + pecado y + pecado X = 2 sen X + pecado X + pecado y y
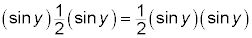
Usted puede cambiar el orden de los términos o factores para hacer que combinan términos más conveniente.
Propiedad asociativa de la suma y la multiplicación: 2 sen X + (pecado X + pecado y) = (2 pecado X + pecado X) Y
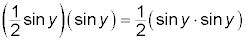
Por reagrupando términos o factores, puede agregar o multiplicar términos que combinan.
Propiedad distributiva de la multiplicación sobre la suma: pecado X(1 - csc X) = Sen X - pecado X csc X. La propiedad distributiva es muy útil, sobre todo cuando se reconoce que uno de los productos que resulta ser una función de los tiempos su recíproco.
Propiedad simétrica:
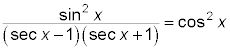
también escrito
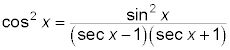
Hacer un flip-flop de las dos partes puede hacer para una mayor comodidad en el trabajo o en la resolución de una ecuación.
Propiedad de multiplicación de ecuaciones: Si
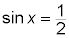
luego 2 sen X = 1. Usted puede multiplicar ambos lados de una ecuación por el mismo número (no sólo 0). Al resolver una ecuación trigonométrica, usted tiene muchas oportunidades ocultas para multiplicar cada lado de una ecuación por 0 o dividir (multiplicar por un recíproco) por 0. La funciones trigonométricas seno, coseno, tangente, cotangente y son 0 para muchas medidas de los ángulos. Simplemente tome esas medidas de los ángulos en cuenta para determinar una solución a la ecuación (en otras palabras, los echan fuera).
La cuadratura un binomio: (pecado X + cos X)2 = Sen2 X + 2 sen X cos X + cos2 X. Uno de los errores más frecuentes que se encuentran cuando cuadrar un binomio es olvidar ese término medio. La cuadratura binomios es especialmente útil en la trigonometría, porque tiende a crear condiciones que son parte de una de las identidades pitagóricas.
Factoring (máximo común divisor): pecado2 X bronceado2 X - bronceado2 X = Tan2 X(pecado2 X - 1). Cuando dos o más términos tienen un factor común, dividiendo cada término por ese factor crea una o más viables expresiones. Sólo asegúrese de dividir todas términos por el factor y para preservar los signos correctos. Al dividir por un factor negativo, las señales de todos los cambian.
Factoring (diferencia de cuadrados): segundo2 X - 1 = (sec X - 1 segundo X + 1). Las identidades pitagóricas todos tienen tres términos al cuadrado en sus ecuaciones. Esto se presta a muchas oportunidades para factorizar como la diferencia de cuadrados. Usted mira hacia adelante para ver lo que puede luego ser dividida en una etapa futura. Otras técnicas de factoring se utilizan con menos frecuencia, pero no dudan en referirse de nuevo a su álgebra para desenterrar algo no mencionado aquí.
Sobre el autor
 Identidades pitagóricas básicos para funciones trigonométricas
Identidades pitagóricas básicos para funciones trigonométricas Las identidades pitagóricas son bloques de construcción para muchas de las manipulaciones de ecuaciones y expresiones trigonométricas. Proporcionan un mayor número de métodos para resolver problemas trigonométricos de manera más eficiente, ya…
 Cotangente y cosecante identidades en un círculo unitario
Cotangente y cosecante identidades en un círculo unitario A partir de la identidad de Pitágoras, el pecado2theta- + cos2theta- = 1, puede derivar cotangente y cosecante identidades pitagóricas. Todo lo que hacemos es tirar un poco de álgebra y aplicar las identidades recíprocas y de relación y -…
 Cómo factorizar expresiones trigonométricas por agrupación
Cómo factorizar expresiones trigonométricas por agrupación El proceso de factoring mediante la agrupación de las obras en casos muy especiales, cuando la expresión trigonometría original es el resultado de multiplicar dos binomios juntos que tienen algunos términos no relacionados en ellos.…
 Cómo factorizar expresiones trigonométricas con títulos superiores a 2
Cómo factorizar expresiones trigonométricas con títulos superiores a 2 Aunque factoring cuadráticas es una brisa, factoring ecuaciones de trigonometría con grados más altos pueden ser un poco desagradable si usted no tiene una situación agradable, como sólo dos términos o una ecuación de segundo grado similar. A…
 ¿Cómo encontrar la inversa de una función trigonométrica
¿Cómo encontrar la inversa de una función trigonométrica Utilice las funciones trigonométricas inversas para resolver ecuaciones como pecado X = 1/2, sec X = -2, O moreno 2X = 1. En las ecuaciones típicas de álgebra, puede resolver por el valor de X dividiendo cada lado de la ecuación por el…
 Cómo multiplicar a través de una ecuación trigonométrica con otra función
Cómo multiplicar a través de una ecuación trigonométrica con otra función La técnica de multiplicar a través de una ecuación de trigonometría por una función selecta no debe ser su primera opción - o su segunda, tercera o cuarta opción. Este método suele ser el último recurso. No es que el método es…
 ¿Cómo resolver una ecuación de trigonometría factorizando cuadráticas
¿Cómo resolver una ecuación de trigonometría factorizando cuadráticas Ecuaciones cuadráticas son agradables de trabajar porque, cuando no factor, puede resolverlos mediante el uso de la fórmula cuadrática. Los tipos de ecuaciones trigonométricas cuadráticas que puede factores son los que, como bronceado2 X = Tan…
 ¿Cómo resolver una ecuación trigonométrica que tiene múltiples funciones trigonométricas
¿Cómo resolver una ecuación trigonométrica que tiene múltiples funciones trigonométricas Algunas ecuaciones de trigonometría contienen más de una función trigonométrica. Otros tienen mezclas de múltiples ángulos y ángulos individuales con la misma variable. Algunos ejemplos de tales ecuaciones incluyen 3cos2 X = Sen2 X, 2 seg X =…
 Cómo cuadrar ambos lados de una ecuación trigonométrica
Cómo cuadrar ambos lados de una ecuación trigonométrica Cuando la resolución de ecuaciones de trigonometría, más de un método generalmente funciona - a pesar de un método es a menudo más rápido o más fácil que otro. Con la práctica, usted obtendrá buenos en la elección de la mejor de las…
 Seno y coseno identidades pitagóricas en un círculo unitario
Seno y coseno identidades pitagóricas en un círculo unitario Si alguna vez se preguntó por qué la identidad de Pitágoras, el pecado2theta- + cos2theta- = 1, es tan importante, y de dónde viene, entonces sigue leyendo. Esta identidad es importante porque establece una expresión que involucra funciones…
 Reorganizar las identidades pitagóricas
Reorganizar las identidades pitagóricas Familiarizarse con las diferentes versiones de las identidades pitagóricas es útil para que pueda reconocer fácilmente en la resolución de ecuaciones de trigonometría o simplificar expresiones.Todas estas diferentes versiones tienen sus…
 Identidades trigonométricas recíprocas
Identidades trigonométricas recíprocas El trig más simple y básica identidades (ecuaciones de equivalencia) son las que implican los inversos de las funciones trigonométricas. Para refrescar la memoria, un recíproco de un número es 1 dividido por el número - por ejemplo, el…