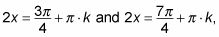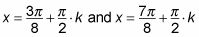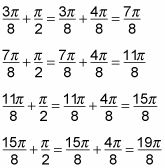¿Cómo encontrar la tangente de un ángulo de doblado
La fórmula de doble ángulo de la tangente se usa con menos frecuencia que las fórmulas de doble ángulo de seno o cosine- sin embargo, no se debe pasar por alto simplemente porque no es tan popular como sus contrapartes más frescas!
La fórmula de doble ángulo de la tangente se deriva reescribiendo moreno 2X tan tan (X + X) Y luego aplicando la fórmula de suma. Sin embargo, la fórmula de doble ángulo de la tangente es mucho más complicado aquí porque se trata de fracciones. Así que usted debe simplemente memorizar la fórmula.
La identidad de doble ángulo de la tangente es
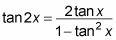
Cuando la resolución de ecuaciones de la tangente, recuerda que el plazo para la función tangente es pi. Este detalle es importante - especialmente cuando se tiene que hacer frente a más de un ángulo en una ecuación - porque por lo general tiene que encontrar todas las soluciones en el intervalo [0, 2pi). Ecuaciones doble ángulo tienen el doble de soluciones en ese intervalo como ecuaciones de ángulo único hacen.
Siga estos pasos para encontrar las soluciones para 2 moreno 2X + 2 = 0 en el intervalo [0, 2pi):
Aislar la función trigonométrica.
Restar 2 a ambos lados para conseguir 2 moreno 2X = -2. Divide ambos lados de la ecuación por 2 siguiente: moreno 2X = -1.
Resolver por el doble de ángulo mediante el uso de la unidad de círculo.
En la unidad de círculo, la tangente es negativa en el segundo y cuarto cuadrantes. Por otra parte, la tangente es -1 en
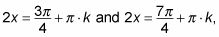
dónde k es un número entero.
Nota: Usted tiene que agregar pi multiplicado por k a cada solución para encontrar todas las soluciones de la ecuación.
Aislar la variable.
Dividir ambos lados de la ecuación por 2 para encontrar X. (Recuerde que usted tiene que dividir tanto el ángulo y el período por 2.) Este paso le da
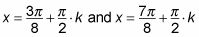
Buscar todas las soluciones en el intervalo requerido.
Continúe agregando pi / 2 a (3pi) / 8 y (7pi) / 8 hasta obtener todas las soluciones de la ecuación que se encuentran en el intervalo [0,2pi). Por supuesto, primero debes encontrar un denominador común - en este caso, 8. A partir de (3pi) / 8:
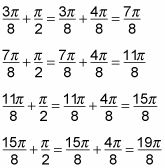
Sin embargo, (19pi) / 8 no se encuentra en el intervalo [0,2pi). Así que deja de aquí y esta solución no se considera. Por lo tanto las cuatro soluciones hasta ahora son (3pi) / 8, (7pi) / 8, (11pi) / 8, y (15pi) / 8. Ahora debe seguir el mismo proceso que el anterior principio con (7pi) / 8. Pronto observar que después de este proceso que comienza con (7pi) / 8 no te llevará a ningún soluciones adicionales. Por lo tanto las cuatro soluciones enumeradas son todas las soluciones en el intervalo [0, 2pi).
-
Encontrar las intersecciones de las líneas y las parábolas - Los fundamentos de la resolución de ecuaciones de álgebra i
-
Cómo calcular un ángulo utilizando funciones trigonométricas inversas -
Cómo calcular la tangente de un ángulo -
¿Cómo combinar los ángulos de referencia con otras técnicas para resolver ecuaciones trigonométricas -
¿Cómo encontrar el seno de un ángulo de doblado
¿Cómo encontrar la tangente de la suma o diferencia de ángulos Al igual que con seno y coseno, usted puede confiar en fórmulas para encontrar la tangente de una suma o una diferencia de ángulos. La principal diferencia es que no se puede leer tangentes directamente de las coordenadas de los puntos en el…
¿Cómo resolver un triángulo cuando se sabe de dos longitudes de los lados consecutivos (ssa) En algunos problemas trigonométricas, se le puede dar dos lados de un triángulo y un ángulo que no es entre ellos, que es el caso clásico de la SSA, o Lado-Lado-Ángulo. En este escenario, es posible que tenga una solución, dos soluciones, o…
Cómo utilizar un ángulo de referencia para encontrar ángulos de soluciones En pre-cálculo, a usar funciones trigonométricas para resolver ecuaciones algebraicas. Cuando encuentre el valor del ángulo en una ecuación, que es el ángulo que es una solución a la ecuación, se utiliza que como el ángulo de referencia para…
Cómo utilizar identidades medio ángulo para evaluar una función trigonométrica Puede utilizar identidades-medio ángulo para evaluar una función trigonométrica de un ángulo que no está en el círculo unitario utilizando uno que sea. Por ejemplo, 15 grados, que no es en el círculo unitario, es la mitad de 30 grados, que se…
Cómo determinar la medida de un ángulo cuyo vértice se encuentra fuera de un círculo Un ángulo que cruza un círculo puede tener su vértice en el interior, sobre o fuera del círculo. Este artículo aborda los tres tipos de ángulos que tienen sus vértices fuera de un círculo: ángulos secante-secantes, ángulos…
Cómo determinar la medida de un ángulo cuyo vértice está en un círculo De los tres lugares vértice de un ángulo puede estar en relación con un círculo (dentro, sobre o fuera del círculo), los dos tipos de ángulos que tienen su vértice en un círculo - inscrito ángulos y ángulos tangente-acordes - son los que…
Funciones Gráfico tangentes con multiplicadores variables En trigonometría, multiplicando el ángulo variable en una función tangente tiene el mismo efecto como lo hace con funciones seno y coseno - que afecta el periodo de la función. Si el múltiplo es 2, como en y = Tan 2X, a continuación, la…
¿Cómo encontrar identidades medio-ángulo para tangente La media de ángulo trig identidad para tangente tiene dos versiones. En lugar de que esto sea una molestia, que tiene más de una opción es realmente bastante agradable, porque se puede elegir la versión que mejor se adapte a su situación. Las…
Encontrar la función de la trigonometría de un ángulo en un círculo unitario Puede determinar las funciones trigonométricas de cualquier ángulo que se encuentran en el círculo unitario - cualquiera que se grafican en posición estándar (es decir, el vértice del ángulo está en el origen, y el lado inicial se encuentra…
¿Cómo resolver una ecuación de trigonometría utilizando la fórmula cuadrática Cuando el factor trigonometría ecuaciones de segundo grado, la vida es buena. Cuando no lo hacen, usted todavía puede sobrevivir, gracias a que la fórmula cuadrática maravilloso. En caso de que hayas olvidado la fórmula exacta, aquí está.La…
Cómo cuadrar ambos lados de una ecuación trigonométrica Cuando la resolución de ecuaciones de trigonometría, más de un método generalmente funciona - a pesar de un método es a menudo más rápido o más fácil que otro. Con la práctica, usted obtendrá buenos en la elección de la mejor de las…
Cómo utilizar la identidad de doble ángulo para el seno La fórmula de doble ángulo para el seno proviene del uso de la identidad trigonométrica para el seno de una suma, el pecado (alfa + beta-) = sinalpha-cosbeta- +-cosalpha sinbeta-. Si alfa = beta-, entonces se puede sustituir beta- con alfa en la…