Cómo determinar la medida de un ángulo cuyo vértice está en un círculo
De los tres lugares vértice de un ángulo puede estar en relación con un círculo (dentro, sobre o fuera del círculo), los dos tipos de ángulos que tienen su vértice en un círculo - inscrito ángulos y ángulos tangente-acordes - son los que se presentan en la mayoría de los problemas y por lo tanto son los más importantes.
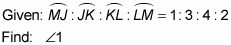
Ángulo inscrito: Un ángulo inscrito, al igual que el ángulo BCD en la figura de arriba a la izquierda, es un ángulo cuyo vértice se encuentra en un círculo y cuyos lados son dos cuerdas del círculo.
Ángulo Tangente-acorde: Un ángulo tangente-acorde, como el ángulo JKL en la figura de arriba a la derecha, es un ángulo cuyo vértice se encuentra en un círculo y cuyos lados son una tangente y una cuerda del círculo.
Medida de un ángulo en un círculo: La medida de un ángulo inscrito o un ángulo tangente-acorde es una mitad la medida de su arco interceptado.
Por ejemplo, en la figura anterior,
Asegúrese de recordar la idea simple que un ángulo en un círculo es la mitad de la medida del arco intercepta (o si usted lo mira a la inversa, la medida de arco es el doble del ángulo). Si se le olvida que es la mitad de los cuales, intente esto: Dibuje un boceto rápido de un círculo con un 90 # 176- arco (una cuarta parte del círculo) y un ángulo inscrito que intercepta el 90 # 176- arco. Vas a ver de inmediato que el ángulo es menor que 90 # 176-, que le dice que el ángulo es lo que es la mitad del arco, no al revés.
Ángulos congruentes en un círculo:
Si dos ángulos inscritos o tangente-acordes interceptan el mismo arco, entonces son congruentes (ver la figura de abajo a la izquierda).
Si hay dos o inscrita tangente acorde ángulos interceptan arcos congruentes, entonces son congruentes (ver la figura de abajo a la derecha).
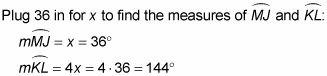
Es hora de ver estas ideas en acción.
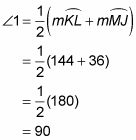
El uso de la figura anterior, resolver el siguiente problema:
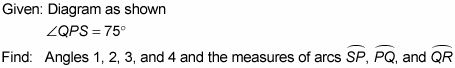
La clave de este problema es que sólo tiene que utilizar la fórmula ángulo inscrito y otra vez. Recuerde - el ángulo es la media de arco del arco es dos veces el ángulo.
Usted tiene las medidas de los tres primeros: 110 # 176-, 176- 40 # y 120 # 176- respectivamente. Eso se suma a 270 # 176-.
Nota: Esta idea de triángulo también te da una buena manera de comprobar sus resultados - hacen los ángulos suman 180 # 176-?
Eso no suman 180 # 176-, lo que comprueba, lo que conduce a la siguiente punta.
Siempre que sea posible, compruebe sus respuestas con un método que es diferente de su método de solución original. Esto es un mucho verificación más eficaz de los resultados de simplemente ir a través de su trabajo por segunda vez en busca de errores.
Familiarización con ángulos Los ángulos son uno de los elementos básicos de los triángulos y otros polígonos de construcción. Hay cinco tipos de ángulos: agudo, recto, obtuso, recto, y el reflejo. Usted ve ángulos en casi todas las páginas de cualquier libro de…
Cómo determinar la longitud de un arco La longitud de un arco significa la misma longitud que el sentido común siempre significa - usted sabe, al igual que la longitud de un trozo de cuerda (con un arco, por supuesto, sería una pieza curvada de cadena). Asegúrese de no mezclar hasta…
Cómo determinar la medida de un ángulo cuyo vértice se encuentra fuera de un círculo Un ángulo que cruza un círculo puede tener su vértice en el interior, sobre o fuera del círculo. Este artículo aborda los tres tipos de ángulos que tienen sus vértices fuera de un círculo: ángulos secante-secantes, ángulos…
Cómo determinar la medida de un ángulo cuyo vértice se encuentra dentro de un círculo Un ángulo que cruza un círculo puede tener su vértice en el interior, sobre o fuera del círculo. Este artículo cubre los ángulos que tienen su vértice dentro de un círculo, los llamados acorde acordes ángulos. La medida de un ángulo de…
Interior y ángulos exteriores de un polígono Todo lo que necesita saber acerca de un polígono no necesariamente comprendido en sus lados. Usted puede necesitar para encontrar ángulos exteriores, así como ángulos interiores cuando se trabaja con polígonos:Ángulo interior: Un ángulo…
Seis teoremas círculo importantes Los seis teoremas círculo discutidos aquí son sólo variaciones sobre una idea básica sobre la interconexión de los arcos, ángulos centrales y acordes (las seis se ilustran en la siguiente figura):Ángulos centrales y arcos:1.Si dos ángulos…
Trabajando con más de una transversal Cuando un dibujo de líneas paralelas-with-transversal contiene más de tres líneas, la identificación de ángulos congruentes y complementarias puede ser un poco difícil. La siguiente figura muestra dos líneas paralelas con dos transversales.Si…
Ángulos en un círculo Hay varias maneras de dibujo un ángulo en un círculo, y cada uno tiene una forma especial de calcular el tamaño de ese ángulo. Cuatro tipos diferentes de ángulos son: central, inscrito, interior, y exterior. Aquí, verá ejemplos de estos…
Acordes frente tangentes de los círculos Usted muestra el diámetro y el radio de un círculo dibujando segmentos a partir de un punto en el círculo, ya sea hacia oa través del centro del círculo. Sin embargo, otras dos figuras rectas tienen un lugar en un círculo. Una de estas figuras…
Cómo calcular funciones trigonométricas usando cualquier círculo Cuando la determinación de los valores de la función trigonométrica de ángulos graficadas en la posición estándar en un círculo cuyo centro está en el origen, usted no tiene que tener un círculo unitario para calcular coordenadas. Puede…
Encontrar la función de la trigonometría de un ángulo en un círculo unitario Puede determinar las funciones trigonométricas de cualquier ángulo que se encuentran en el círculo unitario - cualquiera que se grafican en posición estándar (es decir, el vértice del ángulo está en el origen, y el lado inicial se encuentra…
Cómo localizar ángulos de referencia Cada uno de los ángulos en un círculo unidad tiene un ángulo de referencia, que es siempre un ángulo agudo positivo (excepto los ángulos que ya son positivas y aguda). Al identificar el ángulo de referencia, se puede determinar los valores de…