Encuentre el área de un triángulo con asa
Cuando se tienen dos ángulos en un triángulo y el lado entre ellos (ASA), puede utilizar trigonométrica para hallar el área del triángulo. Las fórmulas van como sigue.
En el triángulo Abecedario, si las medidas de los lados son la, b, y c frente a los respectivos ángulos, entonces se puede determinar el área mediante el uso de una de las siguientes ecuaciones:
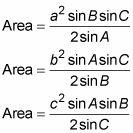
Estas fórmulas son en realidad construyen a partir de la fórmula para encontrar el área con SAS (del lado del ángulo lateral), con un poco de ayuda de la ley de los senos. Así es como uno de ellos llegó a ser.
Comience con la norma SAS para el área.
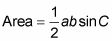
Escribir la ley de los senos que involucran ángulos LA y B.
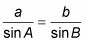
Resolver b.
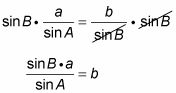
Sustituya el equivalente para b en la fórmula del área.
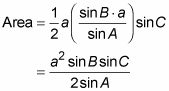
Consideremos ahora un ejemplo. Digamos que tienes un triángulo con ángulos LA, que está a 45 grados, y B, que es 55 grados, y el lado entre ellos, c, igual a 10. Halla el área.
Elija la fórmula correcta - el que tiene c2 en eso.
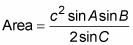
Encuentra los senos de los dos ángulos dados.
El seno de 45 grados es igual a 0,707, y el seno de 55 grados es igual a 0,819.
Encontrar el seno del tercer ángulo.
Ángulo C mide 180 - (45 + 55), o 180 - 100, que es igual a 80 grados.
El seno de 80 grados es igual a 0.985.
Sustituye los valores en la fórmula y resolver.

La zona es un poco más de 29 unidades cuadradas.






